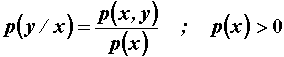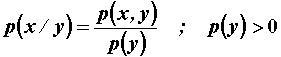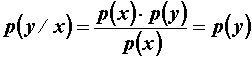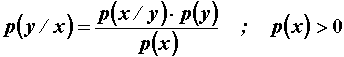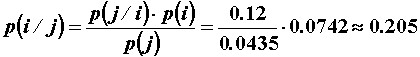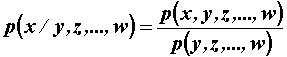11 SLUČAJNI SIGNALI

11.5 Združena i uvjetna vjerojatnost

Promotrimo dvije slučajne varijable X i Y opisane raspodjelama vjerojatnosti p(x) odnosno p(y).

Vjerojatnost združenog događaja X, Y

(11.27)

gdje vrijedi:

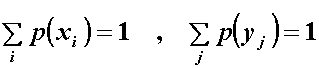
Također će vrijediti:

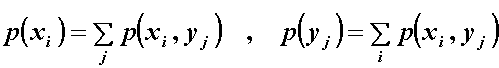(11.28)

Združena raspodjela vjerojatnosti p(x,y) kaže kolika je vjerojatnost da X poprimi vrijednost x_i i da Y poprimi vrijednost y_j.

Primjer 11.3 Bacanje para idealnih kocki X i Y

Varijable X i Y imaju 6 mogućih izlaza:

x_iÎX = (1,2,3,4,5,6), y_iÎY = (1,2,3,4,5,6).

Vjerojatnost p(x_i,y_j) se odnosi na vjerojatnost svih mogućih parova kojih ima ukupno 6×6 = 36. Ako su kocke idealne apriorna vjerojatnost združenih događaja x_i,y_j će biti 1/36. Primjerice p(1,3) = p(1,5) = p(5,6) = ... = p(6,6) = 1/36.

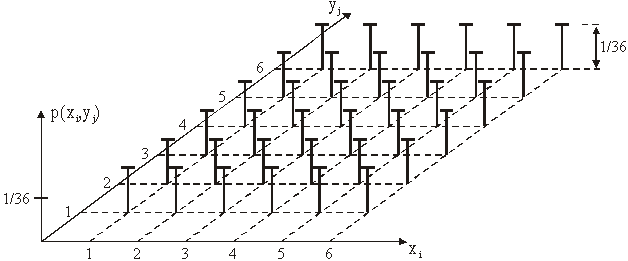
Slika 11.26 Združena raspodjela vjerojatnosti za primjer

bacanja idealnog para kocki

Općenito kad su X i Y neovisne varijable vrijedi:

(11.29)

S druge strane ako su X i Y potpuno ovisni vrijedi p(x,y) = p(x) = p(y). Na primjeru 11.3 potpuna ovisnost bi se ostvarila ako bi se bacala samo jedna kocka a druga kocka bi bila slika kocke u zrcalu.

Uvjetna vjerojatnost

Općenito su varijable X i Y ovisne. Zanimljivo je naći izraz za vjerojatnost da varijabla poprimi vrijednost y ako je varijabla poprimila vrijednost x. Uvjetna se vjerojatnost definira izrazom:

(11.32)

Vrijedi simetrično:

(11.33)

Ako su X i Y potpuo neovisne varijable pa vrijedi (11.29) izraz (11.31) postaje:

što je razumljivo jer Y ne ovisi o X.

Na temelju izraza (11.32) i (11.33) može se također pisati:

(11.34)

Izraz (11.34) je poznat kao Bayesova formula koja je od temeljne važnosti u statistici posebice s primjenom na odlučivanje.

Primjer 11.4 Primjena Bayesove formule

Vjerojatnost slova i i j u tekstu na hrvatskom jeziku su dane u tablici 4.4:

p(i) = 0.0742

p(j) = 0.0435

Neka je poznata vjerojatnost da slovo j dolazi nakon slova i koja iznosi p(j/i) = 0.12. Izračunati uvjetnu vjerojatnost p(i/j).

Rješenje: Na temelju izraza (11.34) slijedi:

Općenito ako slučajna varijabla X ovisi o varijablama Y, Z, ..., W vrijedi:

(11.35)

odnosno analogno izrazu (11.32):

(11.36)

11.6 Zbroj slučajnih varijabli

Zanimljivo je naći izlaz za gustoću vjerojatnosti varijable koja je rezultat zbrajanja dviju ili više slučajnih varijabli.

Uzmimo:

pa se uz poznate p(x) i p(y) traži p(z).

Neka su X i Y neovisne slučajne varijable pa je združena funkcija gustoće vjerojatnosti dana izrazom (11.29):

Gustoća p(z) može biti dobivena analogno relaciji (11.28) preko integrala združene gustoće po jednoj od varijabli:

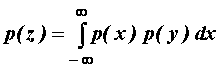
što uz y=z-x daje:

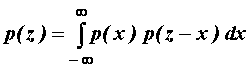(11.35)

Izraz (11.35) predstavlja konvoluciju .

Općenito za zbroj više varijabli vrijedi uz (11.30):

(11.36)

Dakle, funkcija gustoće vjerojatnosti zbroja slučajnih neovisnih varijabli je određena konvolucijom pojedinačnih funkcija gustoće vjerojatnosti.

Primjer 11.5 Raspodjela vjerojatnosti zbroja dviju slučajnih varijabli

U jeziku Matlab pomoću funkcije rand generirana su dva neovisna skupa podataka ravnomjerne raspodjele:

x = rand (n,1)

y = rand (n,2)

Nacrtati raspodjele p(x) i p(y) kao i p(z) = p(x + y).

Rješenje: Raspodjele p(x) i p(y) su ravnomjerne u području (0,1) pa vrijedi slika 11.28. Raspodjela vjerojatnosti zbroja varijabli z = x + y slijedi iz (11.35). Konvolucija dviju pravokutnih funkcija je trokutna funkcija (primjer 12.1) kao na slici 11.28.

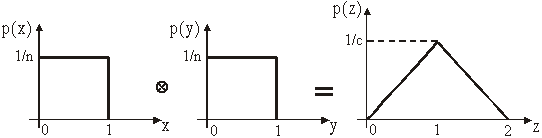
Slika 11.28 Gustoća vjerojatnosti zbroja dviju ravnomjerno raspodjeljenih varijabli je trokutna

Slično zaključku dobivenog kod analize kaskade linearnih sustava (poglavlje 15), kad broj varijabli raste, rezultirajuća gustoća u skladu sa ''središnjim teoremom granične vrijednosti'', postaje Gaussova.

11.8 Skupovi slučajnih signala

Promotrimo izvor slučajnog signala. Primjer takva izvora je generator šuma, signal na priključnici mikrofona ili zvučnika, signal na izlaznoj priključnici videorekordera i slično. Zamislimo da izvor po uključenju polazi od nekih početnih uvjeta, prva generirana poruka će biti neka od poruka x_i. Ako izvor nastavlja po svakom uključenju generirati redom poruku po poruku, može se pisati izlazne poruke npr. x_i(t₁), x_j(t₂), x_k(t₃), ...

Općenito uzmimo da raspodjela p(x;t) nije ista pa nam činjenica da je npr. x_k na izlazu u trenutku t₃ ne pomaže, temeljem eksperimenta, odrediti npr. p(x;t₁). Nužno bi bilo višekratno uključivati izvor na način da uvijek polazi iz istih početnih uvjeta tako da se može eksperimentalno doći do izlaza x_i(t₁), x_j(t₂), x_k(t₃), ... Jednostavnije rješenje problema je u modelu izvora koji ima više izlaza. Svi izlazi su statistički ravnopravni tako da promatrajući izlaze u nekom trenutku t₁, svi izlazi x_i(t₁) su iz iste raspodjele p(x;t₁).

Slika 11.30 ilustrira više istovremenih izlaza iz izvora.

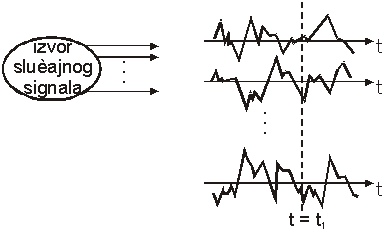
Slika 11.30 Skup slučajnih kontinuiranih signala

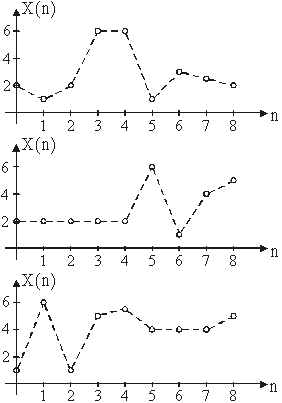
Slika 11.31 Skup slučajnih diskretnih vrijednosti kod bacanja kocke

Iz skupa diskretnih slučajnih signala na slici 11.31, može se odrediti vjerojatnost, npr. da se u prvom bacanju pojavi ‘1’, ‘2’,…, zatim da se u drugom bacanju pojavi ‘1’, ‘2’,…

Vjerojatnost da slučajna varijabla x₁ ima vrijednost iz intervala () u trenutku t₁:

Definiramo stacionarne procese prvog reda za koje vrijedi:

(11.39)

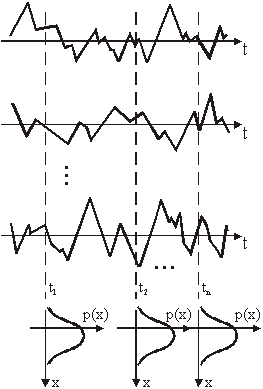
Slika 11.32 Stacionarni slučajni proces

Dakle, za stacionarne procese prvog reda funkcija gustoće vjerojatnosti ne ovisi o trenutku promatranja(slika 11.32).

Općenito se može definirati stacionarnost n-tog reda relacijom:

(11.40)

11.9 Osnove statistike

Statistika podrazumijeva računanje statističkih parametara na temelju vjerojatnosti koje opisuju promatrani slučajni proces.

Primjerice, ako se želi odrediti vrijednost ili simbol koji se najčešće javlja na izlazu izvora, ustvari se želi odrediti tzv. mod raspodjele p(x). Ako je p(x) simetrična funkcija (npr. Gaussova, Laplaceova ili slično), mod je jednak srednjoj vrijednosti ili matematičkom očekivanju.

Ako je poznata funkcija gustoće vjerojatnosti izvora, statistička je srednja vrijednost dana izrazom:

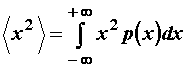(11.44)

Općenito se može definirati srednja vrijednost neke funkcije f(x):

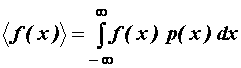
Uz , prosjek definiran gornjim izrazom se u statistici naziva m-ti moment slučajne varijable x. Vrijedi:

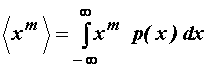(11.45)

Svaki moment varijable x opisuje neko svojstvo raspodjele p(x). Prvi moment (m = 1) definira srednju vrijednost, drugi moment (m = 2) definira srednju vrijednost kvadrata, treći moment definira stupanj asimetričnosti, četvrti moment definira stupanj spljoštenosti, itd.

Za primjenu je posebice važna tzv. varijanca ili disperzija slučajne varijable definirana drugim momentom varijable :

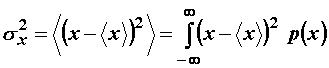(11.46)

Može se pisati:

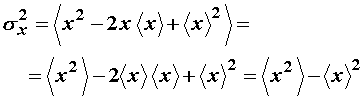
odnosno:

(11.47)

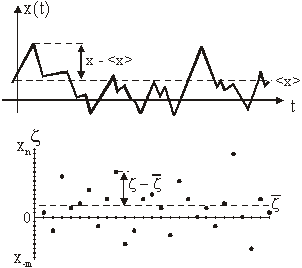
Slika 11.33 Interpretacija varijable (x - <x>) za proračun varijance

za kontinuirane i diskretne procese

Ako je srednja vrijednost slučajne varijable jednaka nuli tj. vrijedi:

Dakle, ako varijabla x nema prosjeka, varijanca je jednaka drugom momentu.

Na sličan način se može definirati statističke parametre za diskretne procese. Srednja vrijednost je:

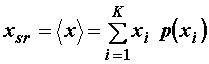(11.48)

odnosno općenito za m-ti moment:

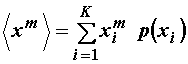(11.49)

Varijanca je diskretna procesa dana izrazom:

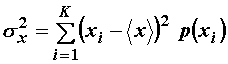(11.50)

Primjer 11.6 Srednja vrijednost normalne gustoće vjerojatnosti

Otpornost otpornika R na temperaturi T je definirana normalnom gustoćom vjerojatnosti:

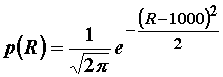
Naći srednju vrijednost otpornosti.

Vrijedi:

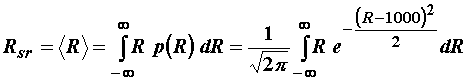
Uz: 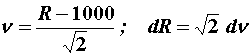, vrijedi:

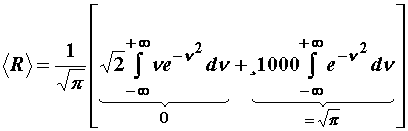
pa slijedi .

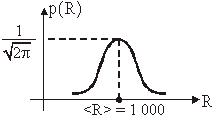
Slika 11.34 Normalna raspodjela R uz

srednju vrijednost <R> = 1000

Rezultat je očekivan zbog definicije normalne funkcije gustoće vjerojatnosti (11.12).

Stacionarni procesi

Općenito prosjek <x> i varijanca slučajne varijable ovise o trenutku promatranja. Za stacionarne procese prvog reda vrijedi (11.39):

(11.51)

tj. raspodjela vjerojatnosti ne ovisi o trenutku promatranja.

Iz (11.51) slijedi:

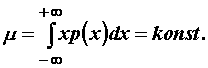
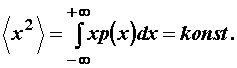
Slučajni proces čija je srednja vrijednost i varijanca konstantna (slika 11.35) je stacionaran proces u širem smislu. Ako se prosjek i varijanca mijenjaju, slučajni proces je nestacionaran (slika 11.36).

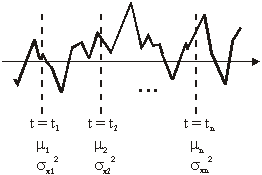
Slika 11.35 Stacionarni slučajni signal

Slika 11.36 Nestacionaran slučajan signal

Prosječna vrijednost <x> i varijanca opisuju svaka na svoj način slučajni proces x(t) u pojedinačnim vremenskim trenucima. Za potpuniji opis slučajnog procesa potrebno je promotriti statističku ovisnost slučajnih varijabli u različitim vremenskim trenucima. Kod toga su od temeljne važnosti autokorelacija i korelacija slučajnih procesa.

11.10 Autokorelacija i korelacija slučajnih procesa

Autokorelacija slučajna procesa se definira izrazom:

(11.52)

Dakle, autokorelacija slučajna procesa predstavlja srednju vrijednost umnoška slučajnih varijabli x(t₁) i x(t₂). Vrijedi:

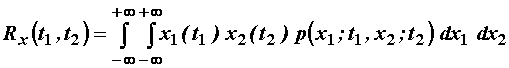(11.53)

gdje je funkcija gustoće vjerojatnosti združene varijable odnosno združena funkcija gustoće vjerojatnosti ili druga gustoća vjerojatnosti (slika 11.37).

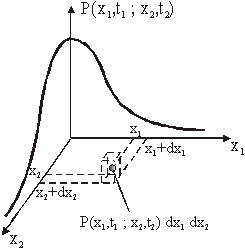
Slika 11.37 Združena gustoća vjerojatnosti

Za stacionarne se procese može pisati: pa vrijedi:

(11.54)

što uz (11.53) daje:

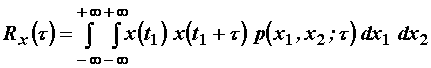(11.55)

ili jednostavno:

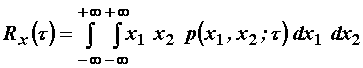(11.56)

Dakle za stacionarne procese, autokorelacija ovisi samo o razlici (kašnjenju) .

Za diskretne stacionarne slučajne procese izraz (11.56) postaje:

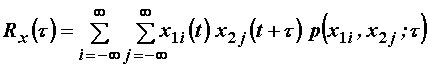(11.57)

ili jednostavno:

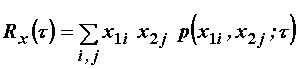(11.58)

Uz iz (11.55) slijedi:

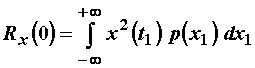(11.59)

pa u skladu s (11.46) vrijedi:

(11.60)

Uz iz (11.45) slijedi:

(11.61)

Dakle autokorelacija uz kašnjenje nula je jednaka varijanci procesa ako je .

Napomena: U primjenama je zanimljiva pored autokorelacije tzv. autokovarijanca. Za razliku od autokorelacije, autokovarijanca se odnosi na slučajne varijable čiji je prosjek jednak nuli:

Analogno izrazu (11.53) može se pisati izraz za korelaciju stacionarnih slučajnih procesa x(t) i y(t):

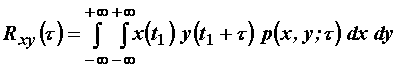(11.62)

Primjer 11.8 Autokorelacija slučajna telegrafskog signala (Poissonov signal):

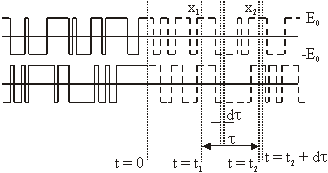
Slika 11.38 Slučajni telegrafski signal

Slika 11.38 prikazuje primjer diskretna slučajnog procesa. Broj prolazaka kroz nulu n tijekom vremena je određen Poissonovom raspodjelom vjerojatnosti:

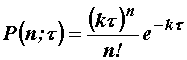(11.63)

gdje je k prosječan broj prolazaka kroz nulu u jedinici vremena.

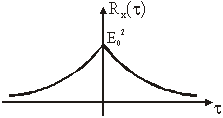
Slika 11.40 Autokorelacija telegrafskog signala

Grafička interpretacija autokorelacijske funkcije

Promotrimo stacionaran slučajan proces x(t). Vrijednost autokorelacije za slučajne varijable x₁ i x₂ u trenucima t₁ i t₂ može se grafički interpretirati na temelju slike 11.41.

Promatramo vrijednosti gdje i označava i-ti član skupa slučajnih signala. Na temelju promatranja na cijelom skupu može se crtati graf x₂ = f(x₁) kao na slikama 11.42 i 11.43.

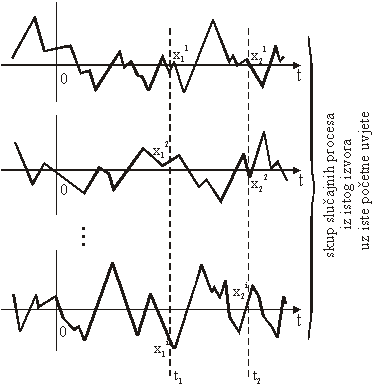
Slika 11.41 Skup slučajnih signala

koji opisuje slučajni signal

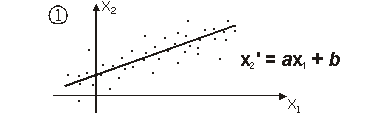
Slika 11.42 Grafički prikaz za autokorelacije:

pozitivna ovisnost x₂ i x₁

Slika 11.43 Grafički prikaz za autokorelaciju: neovisni x₂ i x₁

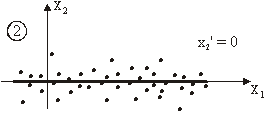
Slika 11.43 predstavlja slučaj potpuno neovisnih slučajnih varijabli x₁ i x₂. Ako takva slika vrijedi za svaki , slijedi:

(11.72)

odnosno:

Proces za koji vrijedi (11.72) naziva se bijeli šum. Slika 11.37 prikazuje autokorelaciju takva bijela šuma.

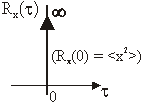
Slika 11.44 Autokorelacija bijela šuma

Graf na slici 11.42 predstavlja opći slučaj. Pravac je određen interpolacijom svih parova točaka (x₁,x₂) pravcem odnosno polinomom prvog reda. Interpolacija se temelji na minimizaciji srednje kvadratne pogreške dane izrazom:

Na temelju kriterija minimalne e, može se pisati:

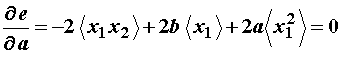
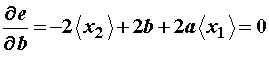
Uz slijedi:

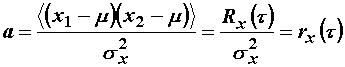(11.73)

(11.74)

gdje je normalizirana autokorelacija. Vrijednosti i su naravno ovisne o izuzev u posebnoj situaciji ilustriranoj na slici 11.43 kad vrijedi a = 0, b = m.

Očigledno je autokorelacijska funkcija temelj za predviđanje slučajnih procesa jer vrijedi:

(11.75)

Uz poznatu autokorelaciju r_x(t) te uz poznato ishodište prognoziranja x₁(t₁) i m, izraz (11.66) omogućuje proračun vrijednosti koju će najvjerojatnije poprimiti slučajna nakon t vremena.

Npr. uz r_x(t) = - 0.6, x₁(t₁) = 178 i m = 0 slijedi prognoza .

11.11 Ergodični procesi

Slučajan proces je ergodičan ako se s vjerojatnošću jednakoj 1 može srednja vrijednost po skupu zamijeniti srednjom vrijednošću po vremenu (slika 11.45).

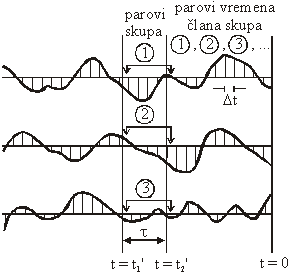
Slika 11.45 Parovi vrijednosti po skupu i parovi po vremenu

Vremenski prosjek slučajnog procesa se definira izrazom:

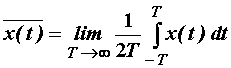(11.76)

Prosjek skupa dan je izrazom (11.44):

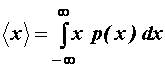
Za ergodičan proces dakle vrijedi:

(11.77)

Primjer 11.9 Sinusni signal slučajne faze

Generator sinusnog signala generira sinusni signal sa fazom koja je slučajan parametar (slika 11.46).

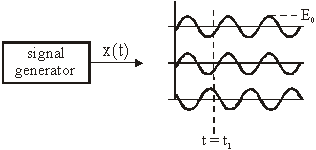
Slika 11.46 Sinusni signal slučajne faze

Vrijedi gdje je slučajna varijabla. Zbog slučajnosti , x(t₁) je slučajna veličina:

Neka je gustoća vjerojatnosti faze ravnomjerna kao na slici 11.47,

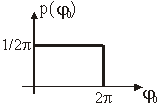
Slika 11.47 Gustoća vjerojatnosti faze sinusnog signala

pa je gustoća vjerojatnosti za slučajnu varijablu x (poglavlje 11.4):

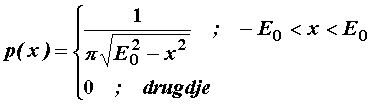
Generator sinusnog signala je u ovom primjeru izvor ergodična procesa jer su prosjeci po vremenu jednaki prosjecima po skupu.

Za ergodične procese, diskretne i kontinuirane, može se iz vremenskog slijeda vrijednosti slučajnog procesa dobiti procjena empiričke vjerojatnosti na temelju relacije:

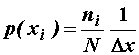(11.78)

gdje n_i kaže koliko puta, u N promatranih trenutaka, vrijednost signala x(t) upada u interval .

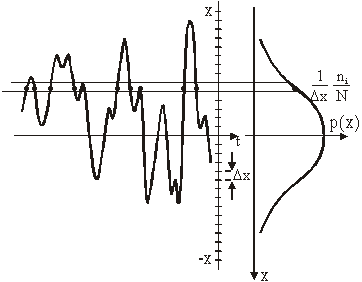
Slika 11.48 Prikaz proračuna empiričke vjerojatnosti

Za ergodične se procese može i autokorelacija pisati preko vremenskog prosjeka. Vrijedi:

(11.79)

ili:

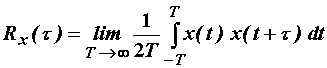(11.80)

Za realne funkcije x(t), je parna funkcija:

Također autokorelacija je kontinuirana svugdje ako je kontinuirana u ishodištu.

Uz vrijedi:

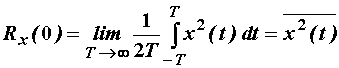
Općenito za ergodične procese vrijedi:

i kad

11.12 Spektralna gustoća snage slučajnih procesa

Fourierova transformacija slučajnog signala x(t) može se definirati izrazom:

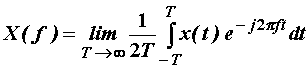(11.81)

Međutim kao što je prikazano na slici 11.50 X(f) izračunata putem (11.81) zadržava statističku neodređenost koja je prisutna kod vremenskog signala x(t).

Slika 11.50 Slučajan signal i njegova FT

Stoga se određivanje spektralne gustoće slučajna procesa može temeljiti ili na prosjeku u vremenskom području ili na prosjeku u frekvencijskom području.

a) Vremenski prosjek kojim se definira determinizam odnosno ovisnost slučajnog signala je autokorelacija. Fourierova transformacija autokorelacije:

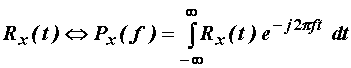(11.82)

gdje P_x(f) predstavlja spektralnu gustoću snage slučajna procesa. je realna pozitivna funkcija, tako da je fazni dio spektra nepoznat. Vrijedi:

Zaključak: Računanjem FT autokorelacije R_x(t) dobiva se spektralna gustoća snage P_x(f).

b) Prosjek u frekvencijskom području se temelji na skupu spektralnih gustoća (slika 11.51). Ako predstavlja gustoću vjerojatnosti za spektralnu gustoću kod frekvencije f=f₁, može se računati prosjek:

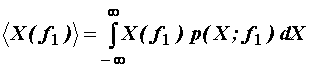(11.83)

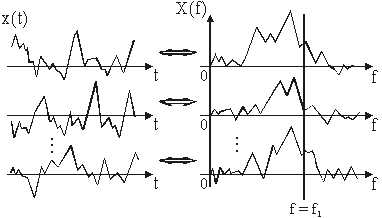
Slika 11.51 Skup signala i skup pripadnih spektralnih gustoća

Ako se izračuna (11.83) za sve f₁ iz područja dobiva se spektralna gustoća amplituda slučajnog procesa |X(f)| dok je prosječna vrijednost faznog dijela jednaka nuli.

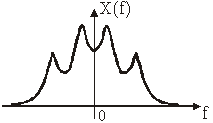
Slika 11.52 Primjer spektralne gustoće

amplituda slučajna procesa

Primjer 11.10 Spektralna gustoća snage 'bijelog' šuma

Autokorelacija bijela šuma je (11.72):

Vrijedi:

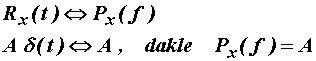
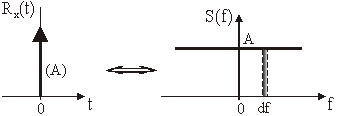
Slika 11.53 Autokorelacija i spektralna gustoća snage bijela šuma

Primjer 11.11 Spektar gustoće snage slučajna telegrafskog signala

Autokorelacija telegrafskog signala je dana izrazom (11.71):

gdje je k prosječan broj prolaza kroz nulu u vremenu t.

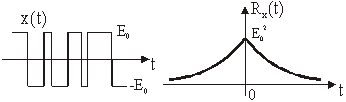
Slika 11.54 Telegrafski signal i njegova autokorelacija

Vrijedi:

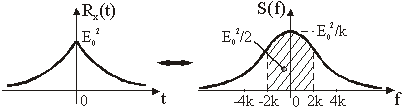
Slika 11.55 Autokorelacija i spektralna gustoća snage telegrafskog signala

11.13 Procjena autokorelacije i spektra slučajnih signala

U praksi je slučajni proces x(t) poznat samo tijekom konačne prošlosti. Na temelju takva signala, ograničena po trajanju, može se govoriti o procjeni autokorelacijske funkcije.

Vrijedi:

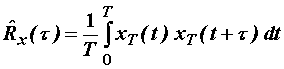(11.84)

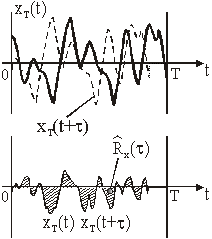
Slika 11.56 Slučajni signal ograničena trajanja i

procjena autokorelacije

Očigledno će procjena autokorelacije , a time i procjena gustoće snage, biti tim bliža točnoj vrijednosti čim je interval T veći. Ovakav zaključak vrijedi i za procese koji nisu ergodični, i gdje se autokorelacija računa preko prosjeka skupa, a odnosi se naravno na broj članova skupa koji su uključeni u račun. Standardna pogreška, kako se može pokazati, je izravno ovisna o trajanju snimanja T, odnosno broju članova skupa N i dana je (uz Normalnu gustoću vjerojatnosti i relativno velike T odnosno N) izrazom:

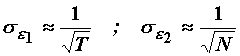(11.85)

gdje su .

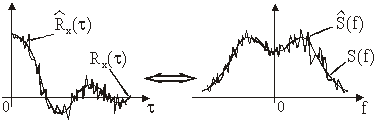
Slika 11.57 Procjena autokorelacije i odgovarajuća procjena spektralne gustoće snage

Slika 11.58 Usporedba procjena autokorelacije bijelog šuma uz T = 1s i T = 100s

Ako se uzme da je pogreška procjene autokorelacije Gaussova varijabla, vrijednost ±2s_e gdje s_eje dana izrazom (11.85) definira područje sigurnosti od 99.5%. Granice ±2s_e kažu da se sve vrijednosti unutar njih mogu smatrati nulom s vjerojatnošću od 95.5% (slika 11.58).

11.14 Detekcija periodična signala u šumu

Osnovni komunikacijski problem je utjecaj šuma (smetnji) zbog čega nastaje gubitak informacije (poglavlje 7). Problem detekcije periodičkih signala u šumu se primjerice javlja kod analize radarskih signala, biomedicinskih signala, kozmičkih signala, seizmičkih signala i slično.

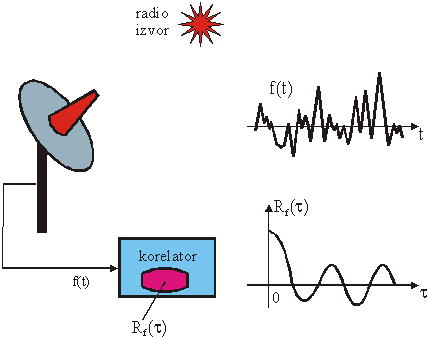
Slika 11.59 Ilustracija problema detekcije signala u šumu

Neka je stacionaran šum n(t) superponiran periodičnom signalu s(t) tako da vrijedi:

(11.86)

Mjera utjecaja šuma na signal se definira ulaznim signal-šum omjerom (SNR) koji predstavlja omjer snaga signala i snage šuma. Ako signali s(t) i n(t) nemaju srednje vrijednosti tj. snage signala i šuma se mogu izraziti preko varijanci, dakle:

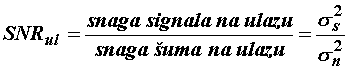(11.87)

Učinkovitost odabrane metode detekcije signala u šumu može se izraziti izlaznim signal-šum omjerom:

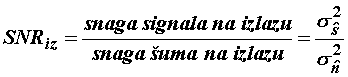(11.88)

gdje je , a je detektirani signal.

Još adekvatnija mjera učinkovitosti je izražena kao dobitak metode koji predstavlja omjer izlaznog i ulaznog signal-šum omjera:

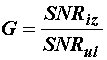(11.89)

Promotrimo sljedeće dvije metode detekcije signala u šumu:

· metoda autokorelacije

· metoda korelacije

a) Detekcija signala metodom autokorelacije

Autokorelacija primljenog signala x(t) je dana izrazom (12.31):

što uz (11.86) daje:

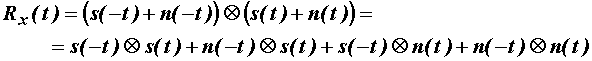
Vrijedi dakle:

(11.90)

gdje su:

Signal s(t) i slučajni šum n(t) nemaju statističke ovisnosti, pa vrijedi:

(11.91)

pa izraz (11.90) na (11.91) postaje:

(11.92)

Budući za stacionarne slučajne signale vrijedi , to će za vrijediti , pa slijedi:

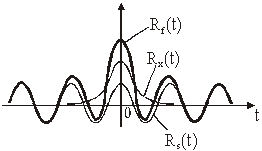
Slika 11.60 Ilustracija izraza (11.92)

Posebno je zanimljiv slučaj kad je n(t) bijeli šum pa vrijedi (11.72):

pa izraz (11.92) postaje:

odnosno:

(11.93)

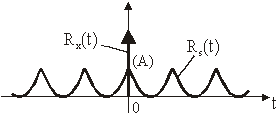
Slika 11.61 Autokorelacija primljenog signala x(t) = s(t) + n(t)

kad je n(t) bijeli šum

Nedostatak opisane metode detekcije putem autokorelacije je u gubitku faze signala pa periodičan signal nije moguće jednoznačno odrediti po obliku.

Određivanje autokorelacije na temelju poznavanja slučajnog procesa u konačnom vremenskom periodu predstavlja problem procjene autokorelacije. Pouzdanost procjene je tim veća što je duže vrijeme mjerenja.

Izlazni signal-šum omjer

Ako se proračun autokorelacije temelji na N uzoraka, izlazni omjer signal–šum je dan izrazom:

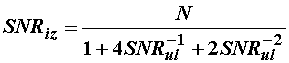(11.94)

ili u decibelima:

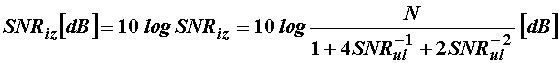
(11.95)

Primjer 11.12 Snaga šuma je dvostruko veća od snage signala

Neka je: pa vrijedi SNR_ul=-3 dB. Dakle, na ulazu u prijamnik s autokorelatorom je slučajan signal dvaput manje snage od snage šuma. Neka je N=16384 pa iz (11.95) slijedi izlazni omjer signal-šum:

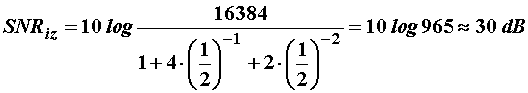(11.96)

Dakle, izlazni omjer snaga signala i šuma je 30 dB što znači da je snaga signala tisuću puta veća od snage šuma. Dobitak postupka je:

(11.97)

Primjer 11.13 Snaga šuma je dvjesto puta veća od snage signala

Neka je pa je SNR_ul = - 23 dB. Iz izraza (11.95) slijedi:

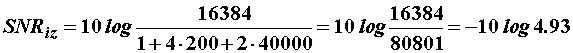
što znači da je na izlazu iz autokorelatora snaga šuma veća od snage signala za oko 5 puta.

Dobitak je postupka u ovom primjeru G » 16 dB. Dobitak općenito ovisi o ulaznom signal-šum omjeru ali i o broju uzoraka N.

Zanimljivo je naći izraz koji definira potreban broj uzoraka uz granični slučaj da su na izlazu signal i šum jednaki.

Uz SNR_iz=0 dB, tj. SNR_iz=1, iz (11.95) slijedi:

(11.98)

Za primjer 11.13 slijedi N₁ = 80801 uzoraka.

b) Detekcija signala metodom korelacije sa slijedom impulsa

Neka je poznat period periodičkog signala T_s. Period signala može biti određen bilo računanjem autokorelacije, bilo pogađanjem kod samog mjerenja korelacije.

Korelacija signala x(t) sa slijedom impulsa perioda T_s je ilustrirana na slici 11.62.

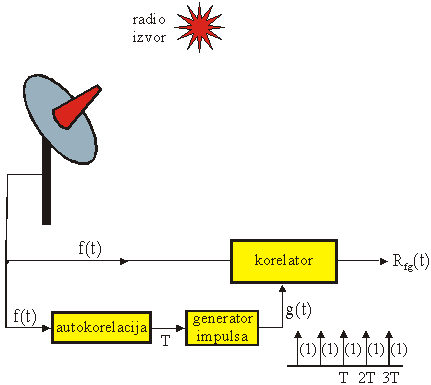
Slika 11.62 Detekcija signala metodom korelacije

Vrijedi:

odnosno:

(11.99)

Šum n(t) i signal g(t) su statistički neovisni dakle: pa (11.99) postaje:

(11.100)

Nađimo R_gs(t). Vrijedi prema (12.31):

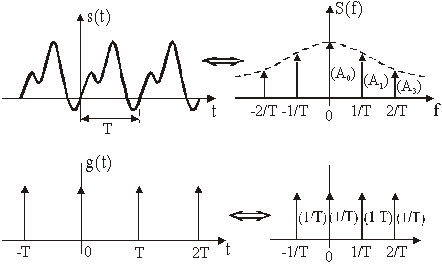
Slika 11.63 Signali i spektralne gustoće

Budući vrijedi:

slijedi:

(11.101)

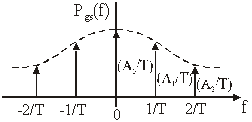
Slika 11.64 Spektralna gustoće korelacije R_gs(t)

Vrijedi dakle:

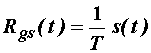
odnosno (11.100) postaje:

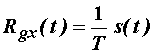(11.101)

Korelacija dakle daje kao rezultat originalni signal.

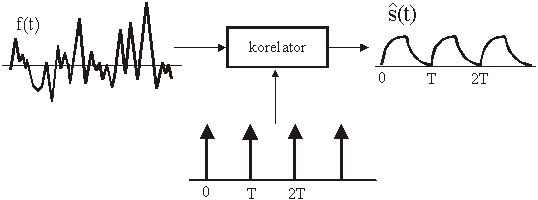
Slika 11.65 Ilustracija korelacije i izlaznog signala

Izlazni omjer signal–šum kod korelacije je dan izrazom:

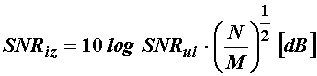(11.102)

gdje je N ukupan broj uzoraka a M je broj perioda signala u okviru N uzoraka.

Na temelju izraza (11.95) i (11.102) može se definirati dobitak koji daje metoda korelacije u odnosu na metodu autokorelacije:

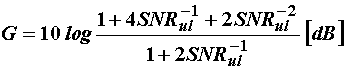(11.103)

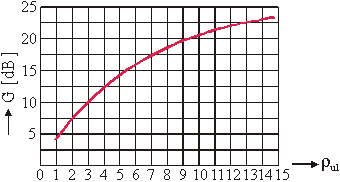
Slika 11.66 Dobitak metode korelacije u odnosu na

metodu autokorelacije

Primjer 11.14 Snaga šuma je dvjesto puta veća od snage signala

Kao u primjeru 11.12 neka vrijedi:

, pa je SNR_ul = - 23 dB

Uz N = 16384 iz (11.102) slijedi:

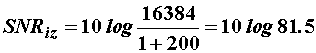
U usporedbi SNR_iz = - 7 dB kod metode autokorelacije dobitak metode korelacije je .

Može se zaključiti da metoda korelacije ima dvojaku prednost u odnosu na metodu autokorelacije: daje veći dobitak i daje originalni signal.

Zanimljivo je spomenuti da se metodom korelacije može odvojeno detektirati više različitih periodičnih signala zahvaljujući činjenici da je korelacija jednaka nuli (poglavlje 10.5).