ODGOVORI NA PITANJA

ODGOVORI NA PITANJA 1

1.

• ponudbeni crtež - prilaže se uz pismenu ponudu

• radionički crtež - crtež prema kojem se izrađuje objekt

• sklopni crtež - prikazuje pojedine sklopove koji sačinjavaju funkcionalnu cjelinu

• instalacijski crtež - prikazuje razvod električnih ili cijevnih vodova

• sastavni ili montažni crtež - prikazuje način sastavljanja cjelovitog uređaja

• situacijski crtež - prikazuje položaj objekta u određenom prostoru

• shematski crtež - pojednostavljani crtež izrađen uporabom simbola i oznaka

• dijagram - grafički prikaz funkcijskih veza različitih veličina

2. Standardne veličine i oblici crteža propisane su da bi se poboljšala preglednost te pojednostavnilo pohranu i rukovanje crtežima. Skup propisanih veličina i oblika za tehničke crteže naziva se format (reda) A.

3.Svojstva formata (reda) A su sljedeća:

• svaki format ima oblik pravokutnika s omjerom stranica je 1 : 2,

• osnovni format je A0 površine 1m²,

• manji format se dobije raspolavljanjem dulje stranice većeg formata.

4.Zaglavlje je tablica u koju se upisuju osnovni podaci o crtežu nužni za njegovu ispravnu uporabu. Oblik i sadržaj zaglavlja nisu jednoznačno određeni. U pravilu sadrži podatke nužne za identifikaciju i razumijevanje sadržaja crteža uključujući:

• naziv crteža (ili predmeta),

• broj crteža,

• naziv tvrtke ili ustanove u kojoj je crtzež izrađen,

• imena i potpise osoba odgovornih za izradbu crteža.

5. Sastavnica je dio tehničke dokumentacije crteža. Ima oblik tablice s podacima nužnim za ispravnu uporabu crteža koji nisu navedeni u zaglavlju. Sadržaj i oblik joj nisu jednoznačno određeni.

6. Zaglavlje se ucrtava u donjem desnom kutu formata koji se postavljaju duljom stranicom vodoravno, a čitavom širinom pri dnu formata koji se postavljaju duljom stranicom uspravno.

Sastavnica se može smjestiti na samom crtežu ili odvojeno. Ako se smješta na crtežu crta se iznad zaglavlja i povezuje s njim. Sastavnica se ispunjava se odozdo prema gore.

7. Pozicijski brojevi povezuju dijelove prikazane na crtežu sa sadržajem sastavnice. Oni se upisuju u sastavnici u za to predviđeni stupac, a na crtežu se upisuju pored dijela koji označavaju. Pozicijski brojevi se na crtežu upisuju dvostruko veći od kotnih brojeva i potcrtavaju se kratkom debelom crtom koja se povezuje tankom crtom s odgovarajućim dijelom crteža. Crta koja povezuje pozicijski broj s dijelom na crtežu naziva se pokazna crta i na samom dijelu završava točkom. Pokazne crte se ne smiju sjeći međusobno, a samo izuzetno mogu se sjeći s mjernim crtama.

8. Općenito primjenjuje se ono mjerilo koje daje jasan crtež prikladan za uporabu. U pravilu se sve veličine s predmeta prenose u istom mjerilu na crtež. Sve projekcije istog predmeta koje tvore cjelinu crtaju se u istom mjerilu. Izuzetno, ako postoji veći broj dijelova i detalja na istom crtežu mogu se primijeniti različita mjerila.

9.

• mjerila za uvećanje: 2:1; 5:1; 10:1; 20:1; 50:1; 100:1

• mjerila za umanjenje: 1:2; 1:5; 1:10; 1:20; 1:50; 1:100

10.Puna crta: vidljivi bridovi predmeta, ograničenje navoja, simboli, okviri tablica,mjernice i pomoćne mjerne crte, šrafura, pokazne crte, crte navoja, dijagonale, mjesta previjanja;

•  Isprekidana crta: zaklonjeni rubovi tijela, zaklonjeni rubovi tijela;

• Crta-točka crta: oznake obrade površine, središnjice, oznake presjeka;

• Prostoručna crta: crte prijeloma i prekida;

• Cik-cak crta: crte prijeloma i prekida;

• Crta-dvotočka crta: granični dijelovi, granični položaji pokretnih djelova.

11. Najčešće korištene crte su crte reda 1.

• Za stupanj širine 1 koriste se širine crta: 1; 0,7; 0,5; 0,35.

• Za stupanj širine 2 koriste se širine crta: 0,5; 0,35; 0,25; 0,18.

12. Znakovi tehničkog pisma mogu se ispisivati pod kutem od 75% ili uspravno. Normom se propisuje:

• nazivna visina H pisma,

• širina crte,

• širina znakova.

Nazivna visina H je visina velikih slova i brojeva. Veličinom H određene su i sve druge dimenzije slova i brojeva.

13. Osnovna svojstva ortogonalne projekcije su:

• bridovi koji su paralelni i jednaki u prostoru zadržavaju ta svojstva i u projekciji,

• kutovi koji su jednaki u prostoru zadržavaju isti odnos i u projekciji.

14.Po smještaju glavnih osi i prikrati u smjeru pojedinih osi razlikuju se sljedeće vrste aksonometrijskih projekcija:

• Izometrija - osi su ravnomjerno razmještene pod kutovima od 120º, nema prikrate u smjeru osiju,

• Dimetrija - dvije osi su pod kutovima od 7º i 90º bez prikrate, a jedna pod kutom od 42º s prikratom 1:2,

• Trimetrija - svaka os ima drugačiji nagib i prikratu,

• Kosa projekcija -  dvije osi su pod kutom od 90º i bez prikrate, a treća je pod kutom od 30º, 45º ili 60º s proizvoljnom prikratom.

15.

16.

17. Kote su djelovi crteža koji sadrže informacije o mjerama predmeta. Kota se sastoji od:

• mjerne crte ili mjernice,

• pomoćne mjerne crte,

• strjelica,

• kotnog broja.

18. Mjerna crta ili mjernica je crta paralelna s dužinom čiju mjeru pokazuje. Mjernicu ne može zamijeniti neka druga crta. Razmak između mjernica i bridova ne smije biti premalen. Razmak između paralelnih mjernica mora biti ravnomjeran i dovoljan za upis brojeva. Križanje mjernica s drugim mjernicama i pomoćnim mjernim crtama treba izbjegavati crtanjem užih kota bliže, a širih dalje od bridova predmeta. Mjernice se nikada ne smiju crtati u smjeru šrafure, nego okomito na njega.

19. Pomoćnim mjernim crtama izvlači se mjera predmeta izvan crteža predmeta. Pomoćna mjerna crta mora prelaziti mjernicu za 1-3 mm. Kad je to prikladnije rješenje može se zamijeniti bridom predmeta. Mogu se križati sa svim drugim vrstama crta osim s mjernicama. Kod malo nagnutih bridova, ako se time poboljšava zornost mogu se izvlačiti i ukoso.

20.

21.

22. Kotni brojevi određuju mjere predmeta. Upisuju se tehničkim pismom iznad mjernica približno po sredini tako da se mogu čitati odozdo i s desna. Svi kotni brojevi na jednom crtežu moraju biti iste veličine. Veličina kotnih brojeva ovisi o nazivnoj širini crte d i iznosi 4-5 d, ali najmanje 2,5 mm. Kotni broj ne smije križati niti jedna druga crta.

23. Strjelice određuju odakle dokle seže mjernica. One ne smiju prelaziti pomoćne mjerne crte ili bridove. Uobičajeno se crtaju unutar pomoćnih mjernih crta ili bridova, a izuzetno, ako nema dovoljno mjesta za njihov smještaj, crtaju se izvana. U slučaju uzastopnog nanošenja kota, kad nema dovoljno mjesta, unutarnje strjelice zamjenjuju se točkom. Dimenzije strjelice ovise o nazivnoj širini crte d.

24. Osnovna pravila za razmještaj kota su:

• Svaka kota se unosi samo jednom i to u onom pogledu ili presjeku koji daje najjasniju predodžbu pojedinog dijela prikazanog predmeta.

• Kote moraju biti raspoređene po svim projekcijama jer svaka prikazuje nešto novo što se mora i kotirati.

• Kote se ucrtavaju na mjestima gdje su najuočljivije.

• Vezane kote, koje se koriste zajedno pri izradbi predmeta, moraju se zajedno i ucrtavati na tehničkom crtežu.

• Kote vanjskog i unutarnjeg oblika predmeta smještaju se na različite strane.

25.

• Kotama se moraju označiti sve mjere potrebne za točnu i jednoznačnu izradbu prikazanog predmeta.

• U pravilu se kotiraju samo vidljivi bridovi predmeta. Izuzetno, u slučaju da se određeni bridovi prikazuju samo kao zaklonjeni mogu se kao takvi i kotirati.

• Crteži standardnih dijelova (koji se ne izrađuju s predmetom nego se nabavljaju kao gotovi dijelovi) na kotiraju se nego se osnovni podaci o njima upisuju u sastavnicu.

26. Pregledne sheme predstavljaju pojednostavljene prikaze uređaja ili sustava koje omogućavaju jednostavno razumijevanje djelovanja. Dijelovi uređaja ili postrojenja prikazuju se simbolima.

27. Strujne sheme predstavljaju detaljan prikaz djelovanja uređaja ili sustava. Elementi i dijelovi uređaja ili sustava prikazuju se simbolima. Strujna shema pruža podatke nužne za održavanje, ispitivanje, te pronalaženje kvara.

28. Nadomjesne sheme predstavljaju pojednostavljene prikaze strujnih krugova koje pružaju podatke na temelju kojih se može provoditi analiza. Pojedini elementi i veličine predstavljaju se simbolima.

29. Grafički simbol predstavlja standardni oblik koji zamjenjuje skupinu istovrsnih elemenata. Pored simbola upisuje se oznaka koja označava i identificira pojedini element. Podaci o različitim svojstvima pojedinih elemenata upisuju se u popise elemenata.

30. Položajni nacrt predstavlje prikaz smještaja dijelova uređaja ili sustava na mjestu ugradnje. Primjeri položajnih nacrta uključuju: smještaj komponenata na tiskanoj pločici, nacrt tiskanih veza, smještaj opreme unutar ormara, smještaj ormara u prostoriji i drugo.

ODGOVORI NA PITANJA 2

1. Što obuhvaća područje računarske grafike?

Računarska grafika (computer graphics) obuhvaća stvaranje, pohranu i uporabu modela i slika objekata. Modeli i objekti računarske grafike potječu iz različitih područja: prirode, znanosti, inženjerstva, apstraktnih koncepata... Posebice, predmet računarska grafike je sinteza slika na temelju računarskih modela stvarnih ili imaginarnih objekata

2. Koja su područja srodna računarskoj grafici?

Procesi analize scene i rekonstrukcije modela objekata predmet su discipline koja se naziva obradba slike (image processing). Obradba slike obuhvaća podpodručja: poboljšanje slike (image enhancement) - razvitak i primjena tehnika poboljšanja kvalitete slike i povećanja kontrasta, detekcije i prepoznavanja uzoraka (pattern detection and recognition) - otkrivanje standardnih uzoraka na slici uključujući npr. optičko prepoznavanje alfanumeričkih znakova (optical character recognition), analizu scene i računalni vid (scene analysis and computer vision) - prepoznavanje i rekonstrukcija 3D modela scene  na temelju više 2D slika.

3. Navedite primjere primjene računarske grafike.

Računarska grafika danas se koristi u različitim područjima gospodarstva, administracije, edukacije, zabave i svakodnevnog kućnog života. Područje primjene se ubrzano širi s rasprostanjenošću računala. Neki primjeri primjene računarske grafike uključuju:

• korisnička sučelja (većina aplikacija na osobnim računalima i na radnim stanicama imaju grafički sustav prozora putem kojeg komuniciraju s korisnicima. Primjeri takvih aplikacija uključuju obradbu teksta, stolno izdavaštvo, proračunske tablice...);

• interaktivno crtanje (u poslovnim, znanstvenim i tehnološkim primjenama računarska grafika koristi se za prikazivanje funkcija, dijagrama, histograma i sličnih grafičkih prikaza sa svrhom jasnijeg sagledavanja složenih pojava i olakšanja procesa odlučivanja);

• uredska automatizacija i elektroničko izdavaštvo (računarska grafika široko se koristi za izradu elektroničkih i tiskanih dokumenata);

• projektiranje pomoću računala (Computer Aided Design - CAD danas se standardno koristi za projektiranje sustava i komponenata u strojarstvu, elektrotehnici, elektronici, telekomunikacijama, računarstvu...);

• simulacija i animacija (računarska grafika koristi se za znanstvenu i inženjersku vizualizaciju i zabavu; područja primjene obuhvaćaju prikaze apstraktnih matematičkih modela vremenski promjenljivih pojava, TV i filmsku tehnologiju...);

• umjetnost (računarska grafika se koristi za kreiranje umjetničkih slika);

• trgovina (računarska grafika se koristi za vizualnu animaciju i elektroničku trgovinu);

• upravljanje procesima (podaci iz senzora dinamički se prikazuju u prikladnom grafičkom obliku);

• geografski informacijski sustavi (računarska grafika koristi se za točan prikaz geografski raspodijeljenih i rasprostranjenih sustava i mjernih podataka npr. u telekomunikacijama i telemetriji);

• grafičko programiranje (računarska grafika se koristi za automatizaciju procesa programiranja virtualnih sustava npr. u instrumentaciji).

4. Kako se grafički sustavi dijele s obzirom na putanju otklonjene zrake?

Tehnologija prikaznih uređaja bitno utječe na arhitekturu grafičkih sustava. U tom smislu razlikujemo dvije osnovne skupine grafičkih sustava:

• vektorski grafički sustavi (sustavi s proizvoljnom putanjom otklonjene zrake),

• rasterski grafički sustavi (sustavi sa sekvencijalnom putanjom otklonjene zrake).

5. Koja je osnovna značajka vektorskih grafičkih sustava?

Pojam “vektor” u terminologiji tehnologije grafičkih sustava označava crtu. Crta koja povezuje dvije (proizvoljno) odabrane točke na zaslonu osnovni je element grafičkog prikaza. Putanja zrake određena je slijedom naredbi iz prikazne liste ili prikaznog programa i povezuje krajnje točke pojedinih crta.

6. Koji su osnovni dijelovi vektorskog grafičkog sustava? Dijelovi vektorskog grafičkog sustava su:

prikazni procesor priključen kao U/I uređaj na glavni procesor (interpretira grafičke naredbe i proslijeđuje koordinate točaka vektorskom generatoru),

• prikazna privremena memorije (sadrži prikaznu listu ili prikazni program),

•  vektorski generator (pretvara digitalne koordinate u analogne vrijednosti napona za otklonski sustav)

• prikazni uređaj.

7. Što je prikazna lista?

Prikazna lista ili prikazni program sadrži niz grafičkih naredbi (npr. za crtanje točaka, crta, znakova). Na kraju je naredba JMP (skok) koja upućuje procesor na početak liste. Procesor ciklički ponavlja naredbe iz prikazne liste frekvencijom od najmanje 30 puta u sekundi i na taj način stvara privid mirne slike jednolikog intenziteta na fosfornom zaslonu koji zadržava osvijetljenost u desetcima ili stotinama mikrosekundi.

8. Opišite sažeto način prikazivanja slika na rasterskim prikaznim uređajima. Rasterski prikazni uređaji pohranjuju primitivne oblike (kao što su crte, alfanumerički znakovi, ispunjene površine) u memoriju u obliku njihovih osnovnih sastavnih slikovnih elemenata - piksela. Cjelovita slika prikazuje se na rasteru koji predstavlja niz paralelnih horizontalnih redova slikovnih elemenata, (ili pravokutnu matricu slikovnih elemenata) koji prekrivaju čitavu površinu zaslona. Pri kreiranju prikaza zraka prolazi preko svih piksela uvijek istim slijedom po svim horizontalnim redovima piksela s lijeva na desno od gornjeg do donjeg horizontalnog reda piksela.

9. Što predstavljaju bitovna matrica i matrica slikovnih elemenata?

Bitovna matrica (bitmap) je matrica čiji elementi (1, 0) predstavljaju svjetloću (ili boju) odgovarajućih elemenata pravokutnog rasporeda osvjetljivih točaka zaslona (slikovnih elemenata) u dvorazinskom sustavu (informacijski kapacitet 1 bit/piksel).

Matrica slikovnih elemenata (pixmap - pixel map) - matrica čiji elementi predstavljaju boju odgovarajućih elemenata pravokutnog rasporeda osvjetljivih točaka zaslona (slikovnih elemenata)  u višerazinskom sustavu (informacijski kapacitet n bit/piksel).

10. Koje su prednosti i nedostaci rasterske grafike?

Prednosti rasterske grafike su:

• jednostavni i jeftini otklonski sustavi (jednostavnije je realizirati otklonski sustav koji uvijek istom putanjom prelazi sve aktivne točke zaslona nego sustav koji može precizno upravljati proizvoljnom putanjom zrake),

• mogućnost prikaza površina ispunjenih bojom ili uzorkom (važno za 3D prikaze),

• neovisnost postupka osvježavanja o složenosti slike.

Nedostatci rasterske grafike su:

• računska složenost (zbog diskretizacije slikovnih prikaza objekata),

• diskretna narav slike (zbog zrnate strukture slike kose i zakrivljene crte su nazubljene ili stepeničaste).

 11. Navedite osnovna svojstva jednostavnog rasterskog grafičkog prikanog sustava.

Osnovna svojstva ove arhitekture su:

• odnos memorije i glavnog procesora je isti kao kod negrafičkih sustava,

• dio memorije služi kao bitovna matrica (fiksni dio, stranice, proizvoljni dio),

• aplikacijski program i grafički paket pohranjeni su u memoriji sustava, a izvodi ih glavni procesor,

• video kontroler prikazuje slike pohranjene u okvirnom međuspremniku,

• video kontroler koji sadrži generator adresa i otklonskih signala adresira lokacije međuspremnika okvira u memoriji, a podaci određuju intenzitet ili boju slikovnih elemenata,

• nedostatak ovakve arhitekture je sporost i veliki broj pristupa memoriji.

12. Kako djeluje video kontroler?

Video kontroler ima zadaću stalnog osvježavanja prikaza. Da bi se izbjegao efekt treperenja osvježavanje se treba obavljati frekvencijom od minimalno 60 Hz. Generator horizontalnih i vertikalnih otklonskih signala usmjerava zraku na određeni slikovni element na zaslovu. Istovremeno generira i horizontalnu i vertikalnu adresu piksela u koordinatnom sustavu zaslona. Na temelju tih koordinata izračunava se linearna adresa (adresa pripadajuće memorijske lokacije) na kojoj se nalaze podaci o svjetloći ili boji slikovnog elementa. Na temelju tih podataka postavljaju se parametri svjetlosnih izvora koji određuju svjetloću ili boju slikovnog elementa.

13. Koja je namjena vidoe pretvorbene tablice?

Zbog uštede memorijskog prostora video kontroler često sadrži pretvorbenu tablicu (look-up table, LUT). Pretvorbena tablica ima onoliko elemenata koliko ima različitih vrijednosti piksela. Vrijednost piksela ne koristi se izravno za upravljanje bojom piksela nego predstavlja pokazivač u pretvorbenu tablicu. Pokazana vrijednost iz pretvorbene tablice upravlja zrakama koje određuju boju piksela na zaslonu.

14. Što podrazumijeva pojam interaktivnosti u računarskoj grafici?

Pojam interaktivnosti u racunarskoj grafici podrazumijeva interakciju izmedu korisnika i sustava na nacin da korisnik upravlja sadržajem, strukturom i pojavom objekta i njegovih predocenih slika uporabom ulaznih uredaja (tipkovnica, miš, zaslon osjetljiv na dodir...).

15. Koje su funkcije i sadržaj aplikacijskog modela?

Funkcije aplikacijskog modela su sljedeće:

• aplikacijski model sadrži sve podatke, objekte i odnose među njima koje koriste prikazni i interakcijski dio aplikacijskog programa ili negrafički moduli za obradu podataka;

• aplikacijski model predstavlja objekte kombinacijom podataka i proceduralnih opisa neovisnih o prikaznom uređaju.

Aplikacijski model sadrži sljedeće:

• primitivne oblike (točka, crta, višekutni likovi u 2D ili 3D, različitih prostornih ploha u 3D...) od kojih je sastavljen model objekta,

• atribute objekata (vrsta crte, boja, struktura površine...),

• odnose među objektima i dijelovima objekata (povezivanje, spajanje...),

• podatke o položaju objekata i dijelova objekata.

16. Koje su funkcije aplikacijskog programa?

Aplikacijski program pretvara opis dijela modela koji treba prikazati u pozive procedura ili naredaba grafičkog sustava koji se koristi za stvaranje slikovnog prikaza u dva koraka:

• pretraživanje aplikacijske baze podataka i izlučivanje podataka nužnih za prikaz odabranog dijela modela,

• pretvorba podataka u format prikladan za ulaz u grafički sustav.

17. Koje su zadaće grafičkog sustava?

Grafički sustav posreduje između aplikacijskog programa i prikaznog uređaja. Zadaće grafičkog sustava su:

• izlazna transformacija (transformira objekt u aplikacijskom modelu u slikovni prikaz modela);

• ulazna transformacija (transformira korisničko djelovanje u ulaznu informaciju za aplikacijski program na temelju kojih aplikacijski program djeluje na promjenu modela i/ili slike).

18. Od čega se sastoji grafički sustav?

Grafički sustav sastoji se od skupa izlaznih podprograma koji odgovaraju različitim primitivnim oblicima, atributima i drugim elementima. Ovi podprogrami tvore biblioteku grafičkih podprograma ili grafički paket i mogu se pozivati iz programskih jezika visoke razine (C, Pascal, LISP). Podprogrami pokreću prikazne uređaje i na taj način generiraju slikovni prikaz geometrijskih primitivnih oblika i atributa specificiranih aplikacijskim programom. Pri tome se koriste logički prikazni uređaji koji razdvajaju razinu aplikacijskog programa od sklopovske razine i razine upravljačkih programa pojedinih uređaja.

19. Što je petlja pokretana događajima?

Tipičan oblik interakcije definirane aplikacijskim programom naziva se petlja pokretana događajima. Petlja predstavlja sekvencijalni automat s konačnim brojem stanja sa središnjim stanjem čekanja. Prijelazi u druga stanja uzrokovani korisničkim ulaznim događajima.

20. Koje su prednosti korištenja grafičkih standarda?

Osnovne prednosti proizlaze iz sljedećih svojstva:

• prenosivost aplikacija neovisno o sklopovlju i operacijskom sustavu,

• prenosivost podataka između aplikacija,

• prenosivost stručnih znanja i vještina.

Krajnji dobitci proizlaze iz smanjenja rada zbog višestrukog korištenja softverskih biblioteka, alata, stručne literature i stečenih iskustava i znanja.

21. Koje su osnovne značajke standarda PHIGS?

Ovim standardom definiran je složeniji grafički sustav s poboljšanom interakcijom i 3D hijerarhijskim strukturiranim modeliranjem. Temeljni koncept je struktura koja predstavlja ugniježdenu hijerarhijsku grupu 3D primitivnih oblika. Standard podupire i dinamičko kretanje: strukture, kao i primitivni oblici mogu se geometrijski transformirati (pomak, zakret, promjena veličine...).

22. Kako je podijeljan grafički sustav prema CGRM modelu?

Po CGRM modelu grafički sustav je podijeljen na 5 jedinica koje se nazivaju okolinama (environments) i to:

• konstrukcijska okolina (Construction Environment) - sadrži grafički model definiran u terminima i jedinicama aplikacije. Operacija kreiranja modela naziva se priprema (Preparation);

• virtualna okolina (Virtual Environment) - grafičku scenu koju sačinjavaju transformacije modela iz konstrukcijske okoline. Operacija transformacije modela u grafičku scenu naziva se produkcija (Production);

• motrišna okolina (Viewing Environment) - sadrži idealnu sliku koja se tvori transformacijom scene iz virtualne okoline s definiranim smjerom gledanja i gledišnom točkom. Operacija transformacije grafičke scene u idealnu sliku naziva se projekcija (projection); 

• logička okolina (Logical Environment) - sadrži sliku koja je priređena uzimajući u obzir osnovna svojstva prikaznih uređaja kao što su minimalna širina crte i broj raspoloživih boja. Operacija transformacije idealne slike u realnu sliku naziva se dovršavanje (Completion);

• realizacijska okolina (Realisation Environment) - sadrži krajnji prikaz potpuno prilagođen prikaznom uređaju. Operacija transformacije slike u prikaz na prikaznom uređaju naziva se prezentacija (Presentation).

23. Koji su logički uređaji definirani standardom GKS?

U GKS standardu definirano je 6 skupina logičkih ulaznih uređaja:

• lokator (locator) omogućava definiranje jedne (x,y) lokacije u koordinatama svijeta,

• lokator niza točaka (stroke) omogućava definiranje niza (x,y) točaka u koordinatama svijeta,

• izbornik primitivnog oblika (pick) omogućava definiranje izlaznog primitivnog oblika,

• izbornik (choice) omogućava definiranje nenegativnog cijelog broja koji određuje izbor iz ponuđenog niza,

• vrijednosnik (valuator) omogućava definiranje realnog broja,

• alfanumerički ulazni uređaj (string) omogućava definiranja niza alfanumeričkih znakova.

24.  Kako se realiziraju logički uređaji definirani GKS standardom?

Navedeni logički uređaji realiziraju se kao stvarni sklopovski uređaji ili kao kombinacija sklopovskih uređaja i grafičke predstave na prikaznom uređaju (npr u obliku potenciometra koji se pokreće pomoću miša). Lokator i izbornik primitivnog oblika se obično implementiraju kao miš (oba pomoću istog miša). Alfanumerički ulazni uređaj implementira se u pravilu putem tipkovnice. Izbornik primitivnog oblika realizira se pomoću digitalizatora.

25. Koji su elementi strukture definirane standardom PHIGS?

Elementi strukture mogu biti sljedeći:

• izlazni primitivni oblici,

• atributi primitivnih oblika,

• specifikacije transformacija,

• podaci o drugim strukturama,

• oznake,

• aplikacijski podaci.

Struktura može sadržavati druge strukture i tako formirati hijerarijsku strukturu.

ODGOVORI NA PITANJA 3

1. Objasnite značenje pojma homogenih koordinata.

Homogena predstava objekta u n-dimenzionalnom prostoru je objekt u (n+1)-dimenzionalnom prostoru. Radi se o nejednoznačnom preslikavanju jer postoji beskonačno mnogo ekvivalentnih predstava objekta iz n-dimenzionalnog prostora u (n+1)-dimenzionalnom prostoru (preslikavanje jednog u mnogo). Vrijednost dodatne koordinate može se proizvoljno odabrati (npr. može imati smisao faktora proporcionalnosti). Inverzno preslikavanje naziva se projekcija (preslikavanje mnogo u jedno). Homogena predstava točke u 2D prostoru (x,y) je homogena točka (x₁,x₂,x₃).

2. Opišite postupak transformacije točke u 3D prostoru.

Ako je općenita transformacija homogene točke u 3D prostoru definirana matricom M tada se njena transformacija može opisati na sljedeći način:

1. homogena predstava točke (x,y,z) u homogenom prostoru je homogena točka  (x₁,x₂,x₃,x₄)

2. koordinate točke transformirane homogene točke  [x’₁  x’₂  x’₃  x’₄ ] određene su sljedećom jednadžbom [x’₁  x’₂  x’₃  x’₄ ] = [x₁ x₂ x₃ x₄ ] M

Transformacija objekta obavlja se tako da se ista transformacija primijeni na sve njegove točke.

3. Napišite matricu translacije koja definira pomak za 3 u horizontalnom smjeru i za 5 u vertikalnom smjeru.

T_x = 3

T_y = 5

4.  Napišite matricu rotacije koja definira zakret točke oko ishodišta za kut od 60°.

Q = 60°

cos Q = 0.5

sin Q = 0.86

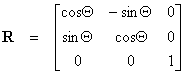
5. Koje su osnovne značajke i vrste ravninskih geometrijskih projekcija?

Ravninske geometrijske projekcije se u načelu odvijaju na način da projekcijske zrake koje izlaze iz projekcijskog središta prolaze kroz sve točke objekta i presjecaju projekcijsku ravninu tvoreći u njoj oblik projekcije. Postoji više vrsta ravninskih geometrijskih projekcija koje su prikladne za različite namjene, a osnovne dvije skupine su perspektivne projekcije i paralelne projekcije. Temeljna razlika je u odnosu projekcijskog središta i projekcijske ravnine. Kod paralelnih projekcija udaljenost projekcijskog središta i projekcijske ravnine je beskonačna, dok je kod perspektivnih projekcija ta udaljenost beskonačna.

6. Na koji način se matematički definira ortogonalna projekcija na xy ravninu?

Ortogonalna projekcija na xy-ravninu odgovara odabiru konstantne vrijednosti z koordinate iznosa 0 tj. z=0. Matematički se ova operacija može definirati kao množenje vektora s dijagonalnom matricom čiji su svi elementi jednaki jedinici osim trećeg koji je jednak nuli.

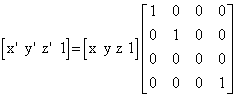
7. Koja je osnovna značajka perspektivne projekcije i kako se ona matematički može definirati?

Kod perspektivne ili fotografske projekcije projekcijske zrake izviru iz jedne točke na konačnoj udaljenosti od projekcijske ravnine. Ako se promatrač se nalazi na udaljenosti h od projekcijske ravnine perspektivna projekcija se može matematički definirati na sljedeći način:

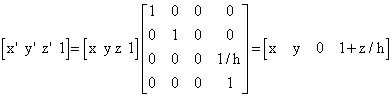
8. Od kojih se koraka sastoji osnovni inkrementalni algoritam za cratnje ravnih crta?

Osnovni inkrementalni algoritam se sastoji od sljedećih koraka:

• proračun nagiba pravca m = Dy/Dx (|m| < 1),

• proračun nove vrijednosti x_i povećanjem prethodne vrijednosti za 1,

• proračun vrijednosti y_i = m x_i + B,

• isticanje piksela (x_i, Round(y_i)) gdje je Round (y_i) = Floor (0.5 + y_i).

9. Na koji način se izbjegava operacija množenja u digitanom diferencijalnom analizatoru?

Množenje se može izbjeći ako se izraz za proračun vrijednosti koordinate y u eksplicitnom obliku jednadžbe pravca napiše na sljedeći način:

y_i+1 = m x_i+1 + B = m (x_i+Dx) + B = y_i + m Dx

Uz  izbor Dx = 1  slijedi  y_i+1 = y_i + m.

10. Na sažet način opišite način izbora sljedeće točke pri crtanju ravvne crte primjenom algoritma središnje točke? Pretpostavimo da je posljednja odabrana točka P s koordinatama (x_p,y_p) te da je potrebno odabrati sljedeću desnu točku. Odabir se svodi na izbor između dviju mogućih točaka: susjedne točke D do koje se dolazi pomakom udesno za jedan i točke GD do koje se dolazi pomakom za jedan udesno i za jedan prema gore. Potrebno je odrediti koja od te dvije točke je bliža idealnom pravcu. Označimo s T točku sjecišta idealnog pravca s dužinom koja povezuje točke D i GD. Izbor sljedeće točke svodi se na određivanje kojoj je od te dvije točke bliža točka T. Prvo se definira središnja točka S(x_p+1, y_p+1/2) kao točka polovišta dužine koja povezuje točke D i GD. Odluka se donosi na temelju informacije o položaju središnje točke u odnosu na idealni pravac. Ako je središnja točka S ispod idealnog pravca onda je očito točka GD bliža idealnom pravcu. Ako je središnja točka S iznad središnje točke onda je točka D bliža idealnom pravcu.

11. Kako se odvija postupak izbora piksela pri ispunjavanju likova?

Izbor piksela koje treba ispuniti odvija se u sljedećim koracima:

• skaniranje po horizontalnim crtama (retcima piksela),

• proračun presjecišta horizontalne i primitivnog oblika inkrementalnim algoritmom (odabiru se točke koje leže unutar oblika),

• poredavanje presjecišta po veličini x koordinate,

• ispunjavanje odsječaka koji leže unutar primitivnog oblika (između neparnih i parnih presjecišta).

12. Zašto su u računarskoj grafici posebno zanimljive aproksimacije krivulja trećeg reda?

Za visoku razinu podudarnosti linearnog aproksimacijskog modela i željene krivulje potreban je velik broj linearnih segmenata. Veća razina podudarnosti odnosno bolja aproksimacija uz manji broj pojedinačnih segmenata može se ostvariti primjenom aproksimacija višeg reda. Na taj način smanjuje se potrebna količina memorije i olakšava interaktivni rad pri modeliranju. Najčešće se koriste aproksimacije trećeg reda jer aproksimacije nižeg reda ne daju dovoljno fleksibilnosti za oblikovanje različitih krivulje, a aproksimacije višeg reda su računski zahtjevnije i složenije za primjenu.

13. Na koji način se definira model krivulje primjenom parametarskih krivulja trećeg reda?

Model krivulje se specificira po odsječcima polinomima trećeg reda. Svaki odsječak Q opisan je s tri funkcije (polinoma trećeg reda) x, y i z parametra t na sljedeći način:

Q(t) = [x(t) y(t) z(t)]

gdje je

x(t) = a_x t³ + b_x t² + c_x t + d_x

y(t) = a_y t³ + b_y t² + c_y t + d_y

z(t) = a_z t³ + b_z t² + c_z t + d_z

uz 0 £ t £ 1.

Ako definiramo vektor potencija parametra t na sljedeći način:

T = [ t³  t²  t  1]

te matricu koeficijenata triju polinoma na sljedeći način:

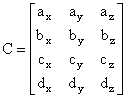
tada možemo pisati izraz za model odsječka krivulje u sažetom obliku

Q(t) = T C.

14. Definirajte pojam geometrijskog kontinuiteta.

Geometrijski kontinuitet G⁰  odgovara  svojstvu neprekinutosti krivulje u točki dodira dvaju odsječaka. Geometrijski kontinuitet G¹  odgovara svojstvu  jednakosti vektora smjera tangente u točki dodira dvaju odsječaka.

15. Definirajte pojam parametarskog kontinuiteta.

Parametarski kontinuitet C¹  odgovara svojstvu jednakosti parametara t u točki dodira dvaju odsječaka. Parametarski kontinuitet Cⁿ odgovara svojstvu jednakosti n-te derivacije Q(t) u točki dodira dvaju odsječaka.

16. Navedite tri vrst eparametarskih krivulja trećeg reda i pripadne geometrijske uvjete.

S obzirom na izbor vrste geometrijskih uvjeta definirane su različite vrste krivulja. Osnovne vrste krivulja su:

• Hermiteove krivulje (uvjeti su: dvije krajnje točke i dva vektora smjera u krajnjim točkama),

• Bezierove krivulje (uvjeti su: dvije krajnje točke i dvije dodatne točke koje određuju vektroe smjera u krajnjim točkama),

• B-krivulje i b-krivulje (uvjeti su: četiri kontrolne točke).

17. Na koji način se mogu pretvarati parametarske krivulje s jednom baznom matricom u parametarske krivulje s drugom baznom matricom?Sve skupine krivulja predstavljene matričnim umnoškom Q(t)=TMG moguće je međusobno pretvarati iz jednih u druge npr. krivulje predstavljenu baznom matricom M₁ i geometrijskim vektorom G₁ moguće je predstaviti drugom baznom maticom M₂ i odgovarajućim geometrijskim vektorom G₂.  Važno je da mora biti ispunjen uvjet:

M₂ G₂= M₁ G₁

Nepoznati geometrijski vektor G₂ može se izračunati na sljedeći način: G₂ =  M₂^-1M₁ G₁

18.  Na temelju kojih kriterija se odabire vrsta parametarskih krivulja trećeg reda?

Kriteriji za izbor vrste krivulje uključuju:

• prikladnost za interaktivnu manipulaciju,

• stupanj kontinuiteta,

• općenitost,

• brzinu proračuna.

19. Kojim geometrijskim uvjetima su definirane Bezierove krivulje?

Bezierove krivulje definirane su sljedećim geometrijskim uvjetima:

• dvije krajnje točke P₁ i P₂.

• dvije kontrolne točke P₃ i P₄ koje određuju vektore smjera u krajnjim točkama R₁ i  R₄. 

Pomoću dviju kontrolnih točaka posredno su definirani vektori smjera tangenti R₁ i R₄ u dvjema krajnjim točkama. Vektor smjera tangente u početnoj točci odgovara derivaciji krivulje Q(t) za vrijednost parametra t=0, dok  vektor smjera tangente u krajnjoj točci odgovara derivaciji krivulje Q(t) za vrijednost parametra t=1.

20. Koji su uvjeti kontinuiteta prvog reda za Bezierove krivulje?

Uvjet za G¹ kontinuitet jest da točke P₃, P₄ i P₅ moraju biti različite i kolinearne

P₃ - P₄ = k (P₄ - P₅),   k > 0

Uvjet  za C¹ kontinuitet jest da je k = 1.

21. Na koji način se odvija iterativni proračun za crtanje parametarskih krivulja?

Iterativni proračun odvija se na način da se vrijednosti koordinanata x(t), y(t), i z(t) pojedinih točaka izračunavaju za niz vrijednosti parametra t međusobno udaljenih za unaprijed određeni konstantan iznos d. Proračunate točke spajaju se ravnim crtama. Problem ovakvog pristupa je u tome što se unaprijed treba odrediti razmak točaka s obzirom na parametar t. Prevelik razmak rezultira slabom kvalitetom aproksimacije dok premalen razmak rezultira nepotrebnim proračunskim opterećenjem.

22. Na koji način se odvija rekurzivna podjela za crtanje parametarskih krivulja?

Rekurzivna podjela odvija se na način da se između dvije izračunate točke umeće treća točka. Rekurzivna podjela zaustavlja se adaptivno kada odsječak krivulje postane dovoljno ravan da se može aproksimirati ravnom crtom. Pojedinosti postupka različite su za pojedine vrste krivulja. Ovaj pristup je posebice prikladan za Bezierove krivulje. Prednost ovog pristupa je u tome što se izbjegavaju nepotrebni proračuni, a nedostatak je što se mora ispitivati ravnoća pojedinih dijelova.

23. Navedite najčešće korištene načine modeliranja površina u trodimenzionalnom prostoru.

Najčešće korišteni načini modeliranja površina u trodimenzionalnom prostoru temelje se na primjeni:

• parametarskih površina,

• mreža višekuta,

• površina drugog reda.

24. Kako se definiraju Bezierove površine trećeg reda?Ako u općem izrazu za dvoparametarsku krivulju trećeg reda uvrstimo Bezierovu baznu matricu M_B i Bezierovu geometrijsku matricu G_B dobivamo izraze za Bezierove površine:

Bezierova geometrijska matrica sastoji se od 16 kontrolnih točaka.

25. Kako se odvija iterativni postupak crtanja dvoparametarskih krivulja trećeg reda?

Iterativni postupak podrazumijeva proračun polinoma trećeg reda za niz bliskih rastućih vrijednosti parametara t i s. Mogući pristup je iscrtavanje niza krivulja kao funkcija parametra t (dok se vrijednost parametra s drži konstantnom za pojedinu krivulju,  a mijenja se od krivulje do krivulje). Zatim se iscrtava niz krivulja kao funkcija parametra s (dok se vrijednost parametra t drži konstantnom za pojedinu krivulju,  a mijenja se od krivulje do krivulje).

26. Kako se odvija rekurzivni postupak crtanja dvoparametarskih krivulja trećeg reda?

Postupak rekurzivne podjele podrazumijeva dijeljenje površine na četverokute (omeđene krivuljama) do zadovoljavajuće ravnoće rezultirajućih četverokuta. Podjela se obavlja dijeljenjem prvo po jednom, a zatim po drugom parametru. Dijeljenje se obavlja crtanjem krivulje po jednom parametru uz konstantnu vrijednost drugog parametra. Konstantna vrijednost drugog parametra određuje se kao aritmetička sredina između vrijednosti tog parametra koje su korištene u prethodnoj podjeli.

27. Što je mreža višekuta?

Mreža višekuta je skup bridova, vrhova i višekuta povezanih tako da oblikuju površinu koja dovoljno dobro aproksimira željenu površinu. Pri tome svaki brid zajednički je za najviše dva višekuta, a svaki vrh zajednički je za najmanje dva brida. Svaki brid povezuje dva vrha. Višekut je zatvoreni skup povezanih bridova (stranica). Postoji više načina za definiranje podataka o mreži višekuta, a temeljna razlika je u odnosu prema dva međusobno suprotstavljena kriterija: minimizaciji memorijskih zahtjeva i minimizaciji računske složenosti.

28. Koje su značajke eksplicitnog  prikaza mreže višekuta?

U eksplicitnom prikazu svaki je višekut predstavljen listom koordinata vrhova:

P = ((x₁, y₁, z₁), (x₂, y₂, z₂), ...,(x_n, y_n, z_n))

Vrhovi su u ovom prikazu poredani redom iscrtavanja. Nedostatak ovog pristupa je u tome što se vrhovi pojavljuju više puta jer ne postoji eksplicitna predstava zajedničkih vrhova. Npr. za pomicanje (npr. pomoću miša) jednog vrha nužno je identificirati sve višekute povezane s tim vrhom. U tu svrhu nužno je usporediti sve koordinate vrhova u jednom višekutu s koordinatama vrhova u svim drugim višekutima. Pored toga i svi zajednički bridovi se iscrtavaju dva puta.

29. Koje su značajke prikaza mreže višekuta temeljenog na strukturi pokazivača na listu vrhova?

U prikazu temeljenom na strukturi pokazivača na listu vrhova svaki vrh se pohranjuje samo jednom u listu vrhova

V = ((x₁, y₁, z₁), (x₂, y₂, z₂), ...,(x_n, y_n, z_n))

Višekut se definira listom pokazivača (indeksa) u listu vrhova. Memorijski zahtjevi su znatno manji nego u eksplicitnom prikazu. Osim toga i promjena koordinata jednog vrha je jednostavna jer nije potrebno uspoređivanje i pretraživanje. Međutim, u ovom prikazu teško je odrediti višekute koji imaju zajednički vrh, a i zajednički bridovi se iscrtavaju dva puta.

30. Kako se vrste elementarnih površine koriste pri modeliranju složenijih površina u računarskoj grafici?

Površine drugog reda kao što su površina kugle, površina elipsoida ili cilindra mogu poslužiti kao elementarne površine za definiranje modela složenijih površina u trodimenzionalnom prostoru. Ova skupina površina definirana je implicitnom jednadžbom oblika:

f(x,y,z) = ax² + by² + cz² + 2dxy + 2eyz + 2fxz + 2gx + 2hy + 2jz + k = 0

Vrsta površine određena je vrijednostima parametara a, b, c, d, e, f, g, h, i, j i k.

Povratak na: Početak stranice | Sadržaj

Inženjerska grafika, Copyright © D.Begusic