13
ANALOGNO-DIGITALNA PRETVORBA
Pretvorba kontinuiranog (analognog) signala u digitalni signal (A/D) i obrnuto (D/A) sastavni je dio suvremenih sustava za obradbu, pohranu i prijenos informacija.
Govorni
signali, signali zvuka (audio) i videa, su kontinuirani po vremenu i po
amplitudi. Pretvorba kontinuiranog signala u digitalni zahtijeva sljedeće
postupke:
·
diskretizaciju po vremenu i/ili
prostoru (uzorkovanje)
·
diskretizaciju po amplitudi (kvantizacija)
·
pretvorbu diskretnih dekadskih
vrijednosti amplitude u digitalnu vrijednost (kodiranje)
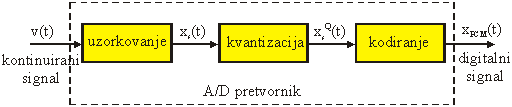
Slika 13.1 Analogno-digitalna pretvorba
A/D
pretvorba predstavlja ustvari kodiranje izvora
(informacije) i to kodiranje uz određeni
gubitak informacije. Gubitak je informacije obično prisutan jedino u
postupku kvantizacije dok postupci uzorkovanja i kodiranja obično predstavljaju
kodiranje bez gubitka informacije.
13.2 Uzorkovanje
Čemu uzorkovanje? Prvo, digitalni sustavi mogu raditi samo s diskretnim i konačnim skupom podataka. Drugo, ako se uzorkovanjem ne gubi informacija, obradba na razini uzoraka, umjesto na razini kontinuiranog signala, znači uštedu. Štoviše, sustavi koji sudjeluju u obradbi, pohrani ili prijenosu informacije, mogu uzorkovanjem biti vremenski raspodjeljeni između više korisnika.
Pretpostavka: Svi realni procesi koje susrećemo u praksi su takvi da
im je spektralna gustoća jednaka nuli (ili je zanemariva) kod i iznad neke
gornje frekvencije fc. Odgovarajući signal x(t) posjeduje dakle
ograničen frekvencijski spektar kao na slici 13.2.
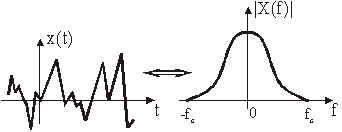
Slika 13.2 Realni slučajni signali imaju ograničen spektar
Vrijedi:
 (13.1)
(13.1)
Zbog njene
posebne važnosti frekvencija fc
se naziva kritična frekvencija signala x(t).
Temeljna su
pitanja:
·
da li se uzorkovanjem, uz povoljno
odabranu frekvenciju fs,
može sačuvati cjelovita informacija sadržana u signalu x(t)?
·
čime je određena frekvencija
uzorkovanja fs koja jamči
cjelovitost informacije?
Odgovori na
ova pitanja proizlaze iz analize spektralne gustoće uzorkovanog signala.
Spektralna
gustoća uzorkovanog signala
Uzimanje
uzoraka iz kontinuiranog signala x(t)
uz vremenski interval Dt može se
interpretirati kao množenje te funkcije sa slijedom impulsa perioda Dt odnosno
frekvencije fs = 1/Dt (slika
13.3).

Slika 13.3 Uzorkovanje kontinuirana signala
Vrijedi:
 (13.2)
(13.2)
Uz
Fourierove transformacijske parove:


izraz (13.2)
postaje:

ili:
 (13.3)
(13.3)
Neka
vrijedi:
 (13.4)
(13.4)
gdje je fc kritična frekvencija a fs je frekvencija uzoraka.
Izraz (13.3)
se može pisati u obliku (poglavlje 12):
 (13.5)
(13.5)
Slijedi da spektralna gustoća Xs(f)
predstavlja periodično ponavljanje X(f) s periodom fs.

Slika 13.4 Grafički prikaz izraza (13.3) i (13.5)
Iz slike
13.4 se može zaključiti da očigledno vrijedi:
 (13.6)
(13.6)
Zaključak: spektralna je gustoća signala uzoraka Xs(f)
jednaka spektralnoj gustoći kontinuiranog signala X(f) (za konstantan faktor fs)
u frekvencijskom području  .
.
Priozlazi da
se originalni kontinuirani signal x(t)
može dobiti iz signala uzoraka xs(t)
prolaskom ovog signala kroz idealni niskopropusni (NF) filtar granične
frekvencije
fg = fs / 2 (slika 13.5). Prijenosna funkcija filtra treba dakle biti:
 (13.7)
(13.7)

Slika 13.5 Originalni kontinuirani signal se dobiva prolaskom signala uzoraka kroz filtar definiran izrazom (13.7)
Zaključak: Uzorkovani signal može sačuvati cjelovitu
informaciju kontinuiranog signala. Uvjet koji treba biti ispunjen je:
frekvencija uzorkovanja fs treba biti barem dvostruko veća od
kritične frekvencije kontinuiranog signala fc tj.:
 (13.8)
(13.8)
Teorem
o uzorkovanju
Impulsni
odziv idealnog NF filtra granične frekvencije fg je dan izrazom:
 (13.9)
(13.9)
Ako je na
ulazu filtra signal uzoraka xs(t),
izlaz x(t) je definiran konvolucijom
(poglavlje 15):
![]() (13.10)
(13.10)
Signal
uzoraka xs(t) se može na
temelju (13.2) pisati:

pa izraz
(13.10) postaje:

Konvolucija
neke funkcije sa impulsnom (Diracovom) funkcijom daje opet tu istu funkciju pa
vrijedi:
 (13.11)
(13.11)
ili uz
granični slučaj ![]() :
:

odnosno:
 (13.12)
(13.12)
Izrazi
(13.11) i (13.12) predstavljaju teorem o uzimanju uzoraka koji kaže: Kontinuirani signal, frekvencijski
ograničena spektra ![]() , može biti bez gubitka informacije zamijenjen signalom
uzoraka ako su uzorci uzeti svakih
, može biti bez gubitka informacije zamijenjen signalom
uzoraka ako su uzorci uzeti svakih ![]() , tako da vrijedi:
, tako da vrijedi:
 (13.13)
(13.13)
Izrazi
(13.8) i (13.13) su jednaki. Izraz (13.8) je rezultat analize a izraz (13.13)
je rezultat sinteze kontinuiranog signala.
Pojava
prekrivanja i njegovo otklanjanje (antialiasing)
Što ako nije
zadovoljen uvjet (13.13) tj. ako je frekvencija uzoraka manja od dvostruke
kritične frekvencije?
Ako dakle
vrijedi:
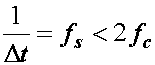
može se
problem razmotriti u frekvencijskom području (slika 13.6). Očito sada vrijedi:

pa se može ustvrditi da je postupkom uzorkovanja
izgubljen dio informacije. Može se
govoriti o tzv. učinku prekrivanja (aliasing efect) koji je posljedica
nedovoljno visoke frekvencije uzoraka.

Slika 13.6 Učinak prekrivanja zbog nedovoljno visoke frekvencije uzorkovanja
Učinak
prekrivanja može biti otklonjen ako se spektralni sadržaj ulaznog kontinuiranog
signala prije uzorkovanja ograniči na polovinu frekvencije uzorkovanja. Ovo se
ograničenje spektra može jednostavno ostvariti prolaskom signala kroz idealni
NF filtar (antialiasing filtar) granične frekvencije fg = fs / 2 kao što je to prikazano na slici
13.7. Na ovaj je način za signal prije uzorkovanja osigurano da kritična
frekvencija iznosi
fc = fs / 2 što jamči sačuvanje cjelovite informacije nakon uzorkovanja.

Slika 13.7 Primjena 'antialiasing' filtra kod uzorkovanja
U praksi se filtriranje koje spriječava pojavu prekrivanja spektara koristi uvijek bez obzira da li je uvjet (13.13) ispunjen čime se otklanja prekrivanje eventualno prisutnog šuma čiji spektralni sadržaj postoji i kod frekvencija iznad kritične frekvencije signala.
Primjer 13.1 Uzorkovanje sinusne funkcije
Zadatak:
Odrediti frekvenciju uzorkovanja sinusnog signala frekvencije f1 = 1000 Hz tako da ne dođe
do pojave prekrivanja.
Rješenje: iz
izraza (13.8) slijedi:
![]()
Ako je f1 = 1000 Hz, kritična
frekvencija fc definirana
izrazom (13.1) mora biti:
![]()
Npr. može se
uzeti fc = 1001 Hz ili
slično. Slika 13.8a prikazuje niz uzoraka uz fs = 2500 Hz > 2fc. Međutim ako bi se
uzela fc = 1000 Hz i fs = 2fc = 2000 Hz
uzorci bi bili kao na slici 13.8b. Očito je 2000
Hz nedovoljno visoka frekvencija.

Slika 13.8 Uzorkovanje sinusna signala frekvencije 1000
Hz
a) dovoljno visoka frekvencija uzorkovanja
fs = 2500 Hz
b) nedovoljno visoka frekvencija
uzorkovanja fs = 2000 Hz
Primjer 13.2 Uzorkovanje složena periodična signala
Zadan je
periodičan signal
![]()
Odrediti:
a)
kritičnu frekvenciju fc
b) analogni signal na izlazu iz filtra na slici 13.5 ako je frekvencija
uzoraka fs = 5000 Hz.
Rješenje:
a)
Najviša frekvencija u signalu je 6000 Hz pa je fc > 6000 Hz (npr. 6001 Hz).
b) Zbog fs = 5000 Hz < 2fc
= 12002 Hz javlja se učinak prekrivanja. Rezultirajući signal se može lako
odrediti na temelju spektra uzorkovanog signala. Na temelju konvolucije kao na
slici 13.6 može se zadani primjer (uz sliku 10.15) lako dobiti (vidi sliku):

Primjer 13.3 Uzorkovanje audio signala (CD-audio)
Spektralni
sadržaj audio signala je određen čujnošću ljudskog uha koja obuhvaća područje
od desetak hertza da 20 kHz. Standardna audio CD kvaliteta obuhvaća područje do
22 kHz čime je definirana kritična frekvencija fc. Frekvencija uzorkovanja audio signala je dakle barem
dvostruko veća od kritične frekvencije i iznosi fs = 44.1 kHz. Slika 13.9 ilustrira uzorkovani signal
trajanja 10 ms signala gitare za
akord D-dur uz fs = 44.1 kHz.
Slika 13.9 Uzorkovani signal gitare uz akord D-dur
Vremensko
multipleksiranje signala (TDM)
Budući se
kontinuirani signal može zamijeniti nizom uzoraka bez gubitka informacije,
vrijeme između uzoraka može biti iskorišteno za obradbu, pohranu ili prijenos
drugih također uzorkovanih signala. U tom slučaju govorimo o vremenski
multipleksiranoj (TDM) obradbi, pohrani ili prijenosu signala. Slika 13.10
ilustrira višestruki (multipleksni) prijenos signala sa vremenskom raspodjelom
putem jednog te istog komunikacijskog kanala. Sustav za uzimanje uzoraka
sinkrono uzorkuje signal po signal s frekvencijom fs uz vremensko kašnjenje DT = 1 / (M fs), gdje je M broj multipleksiranih signala. Frekvencija uzoraka u kanalu je
dakle jednaka M fs.

Slika 13.10 Vremensko multipleksiranje (TDM)
Primjer 13.4 PCM primarni sustav
Vremensko
multipleksiranje se primjenjuje u svim suvremenim komunikacijskim i
informacijskim sustavima. Tipičan primjer je multipleksiranje 32 telefonska
kanala u jedan standardni PCM kanal (link). Frekvencija uzoraka kojom se
uzorkuju telefonski signali iznosi 8 kHz
pa je frekvencija uzoraka u PCM TDM kanalu 32
× 8 = 256 kHz (poglavlje 16).
13.3 Kvantizacija
Vrijednosti
uzoraka uzetih iz kontinuiranog signala su kontinuirane tako da vrijedi:
![]() R (skup svih realnih
brojeva)
R (skup svih realnih
brojeva)
Skup
kontinuiranih vrijednosti R je
beskonačan. Međutim digitalna je obradba signala moguća samo ako je skup
vrijednosti diskretan i konačan zbog čega je potrebna kvantizacija.
Ako se
cijelo područje realnih brojeva R
podijeli u N nepreklapajućih
segmenata Ri (1 £ i £ N) koji predstavljaju kvantizacijske
intervale, pa ako se svakom uzorku čija vrijednost xs upada u interval i
dodijeli određena vrijednost yi
koja predstavlja (zastupa) taj interval, izvršeno je kvantiziranje.
Slika 13.11
prikazuje primjer ravnomjerna kvantiziranja u paran broj razina kod kojeg su
svi segmenti Ri jednaki pa
vrijedi:


![]()

![]()


![]()

gdje je Dx veličina
segmenta ili tzv. korak kvantizacije, a 2V je područje kvantizatora pa je broj kvantizacijskih razina:
 (13.15)
(13.15)

Slika 13.11 Ravnomjerna kvantizacija
Pitamo se šta je sa pogreškom odnosno varijancom
pogreške kvantiziranja. Ako se uzme da je Dx<<V gdje je V = xs(t)| max onda se može pokazati da bez
obzira na funkciju gustoće vjerojatnosti ulaznog procesa pogreška je
ravnomjerno raspodjeljena tako da vrijedi:


Slika 13.12 Pogreška kvantizacije je ravnomjerno
raspodjeljena uz N >> 1
Slijedi varijanca pogreške: (13.15)
(13.15)
Može se dakle općenito reći da proces kvantizacije unosi u kvantizirani
signal šum, pa se definira signal-šum omjer kvantizatora:
 (13.16)
(13.16)
Neka je kvantizator sa N razina
tako da vrijedi:
![]()
pa je korak kvantizacije:
 (13.17)
(13.17)
Ako je varijanca signala ![]() onda V predstavlja dovoljno veliku vrijednost
da se uz danu p(x) vrijednost V premaši u zanemarivom broju slučajeva.
Npr. ako je ulaz Gaussov onda je posve dovoljno uzeti
onda V predstavlja dovoljno veliku vrijednost
da se uz danu p(x) vrijednost V premaši u zanemarivom broju slučajeva.
Npr. ako je ulaz Gaussov onda je posve dovoljno uzeti ![]() .
.
Uz (13.17) izraz (13.15) postaje:
 (13.18)
(13.18)
Ako se uzme da je signal ravnomjerno raspodjeljen vrijedi  pa slijedi izraz za
signal-šum omjer iz (13.16):
pa slijedi izraz za
signal-šum omjer iz (13.16):
 (13.19)
(13.19)
Dakle signal-šum omjer kvantizacije raste s kvadratom broja kvantnih
razina.
U primjenama je prikladan izraz (13.19) definiran u dB:
 (13.20)
(13.20)
gdje je N = 2m, tako
da m odgovara broju bitova po uzorku.
Audio signal CD kvalitete se kvantizira u N = 216 razina (tj. N
= 65536) tako da je broj bitova po uzorku 16. Audio signal je praktički ravnomjerno raspodjeljen pa
signal-šum omjer kvantizacije prema (13.20) iznosi 96 dB. Ova vrijednost je zadovoljavajuća jer se uzima da je
dinamičko područje elektroničkog orkestra 100
dB.
Nelinearna
kvantizacija
Postavlja se pitanje da li je ravnomjerni kvantizator pravo rješenje tj.
postoji li nelinearni kvantizator koji će dati, za zadanu p(x) ulaznog signala, manju varijancu greške kvantizacije. Postupak
nelinearne kvantizacije može se interpretirati putem nelinearne transformacije
i ravnomjerne kvantizacije kao na slici 13.13.

Slika 13.13 Nelinearna kvantizacija
Kakva transformacija T(x) daje
minimalnu varijancu pogreške? Nelinearni element T(x) izvodi transformaciju ulazne
gustoće vjerojatnosti p(x)
u izlaznu p(y). Transformacija T(x) oblika kao na slici 13.13 može se
na temelju izraza (11.26) pisati:

pa vrijedi:
 (13.21)
(13.21)
Iz uvjeta:

slijedi:
 (13.22)
(13.22)
Primjer 13.6 Nelinearna kvantizacija govornog signala
Govorni signali mogu biti dobro opisani Laplaceovom gustoćom:

pa iz (13.22) slijedi optimalna T(x):
 (13.23)
(13.23)
Slika 13.14 prikazuje T(x)
definiranu izrazom (13.23). Očigledno se radi o jako nelinearnoj funkciji.
Linija T(x) = x odgovara slučaju
ravnomjerne kvantizacije koja nije optimalna za govorne signale ali je
optimalna za ravnomjerno raspodjeljene signale.

Slika 13.14 T(x) prema izrazu (13.23)
Ako je signal nestacionaran tj. nema konstantnu varijancu kakvi su
primjerice govorni signali, optimalna T(x)
se mijenja sa varijancom. U takvim se slučajevima koriste ili adaptivni
kvantizatori ili podoptimalni kvantizatori koji uz predviđenu dinamiku daju
povoljniji signal-šum omjer. Primjer podoptimalnih kvantizatora su A i m zakon koji su standardno primjenjeni
kod PCM sustava.
Primjer 13.7 Nelinearna kvantizacija u PCM telefonskim sustavima
Kvantizacija u PCM sustavima se izvodi primjenom T(x) koja je aproksimirana A
ili m zakonom. A zakon je ITU-T standard G.711 koji predstavlja podoptimalnu T(x) koja je uz to i linearizirana po segmentima kao što je
prikazano na slici 13.15. Ukupan broj linearnih segmenata je 13 pa je oznaka
takva kvantizatora A 87.6/13.
Vrijednost 87.6 je vrijednost
veličine A a vrijednost ±1/A definira
prvi linearni segment (oko nule).

Slika 13.15 Nelinearna karakteristika
PCM kvantizatora prema ITU-T G.711
6.4 Kodiranje
Pretvorba
kvantiziranog uzorka u binarnu kodnu grupu odnosno u digitalan signal
podrazumijeva pridjeljivanje dekadskoj vrijednosti uzorka m-člani binarni niz. Ovo je ustvari sažimanje
abecede što je detaljnije opisano u poglavlju 6.3.
Ako je
vrijednost uzorka xk
vrijedi:

gdje je m broj bita tako da vrijedi ![]() a
a ![]() predstavlja binarne
simbole m-torke
predstavlja binarne
simbole m-torke ![]() .
.
Npr. uz xk = 12 vrijedi:

pa je m = 4 a pripadna binarna kodna grupa je (1 1 0 0).
Postupak se
kodiranja može odvijati uzorak po uzorak, bit po bit ili kvant
po kvant.
Postupak
uzorak po uzorak je primjeren većim brzinama primjerice pri kodiranju video
signala. Odgovarajući koder zahtijeva N
komparatora (slika 13.16). Kodiranje jednog uzorka se obavlja odjednom.

Slika 13.16 Koder uzorak po uzorak
Postupak bit
po bit ili tzv. metoda sukcesivne aproksimacije primjerena je nižim brzinama.
Odgovarajući koder zahtijeva ld N
komparatora (slika 13.17). Kodiranje jednog uzorka se obavlja u m koraka.

Slika 13.17 Kodiranje bit po bit
Kodiranje
kvant po kvant predstavlja najsporiji postupak kodiranja, ali i
najjednostavniji jer je potreban samo jedan komparator. Kodiranje uzorka se
obavlja u prosjeku u N/2 koraka.