14 DISKRETNA FOURIEROVA
TRANSFORMACIJA (DFT)
I
FFT ALGORITAM
Uvod
Diskretna
Fourierova transformacija (DFT)
Učinak propuštanja
Optimalne
prozorske funkcije
Brza
Fourierova transformacija (FFT)
Primjene FFT
Diskretna
korelacija i konvolucija putem FFT
14.1
Uvod
U današnjim se primjenama uglavnom koristi digitalna obradba signala. Ako
je ulazni signal kontinuiran, digitalan signal se dobiva putem A/D pretvorbe.
Budući je obradnik digitalan, izlazni signal je također uzorkovan signal.
Ako se radi o računanju FT, to znači da izlaz predstavlja diskretnu (po
frekvenciji) spektralnu gustoću. Ako
je spektralna gustoća nekog signala diskretna onda se nedvojbeno radi o
periodičkom vremenskom signalu (poglavlje
9.3). Ova činjenica je od temeljne važnosti za definiranje svojstava
DFT.
Svaki realan sustav za obradbu signala ima ograničen kapacitet. To znači da
se može računati samo s ograničenim brojem uzoraka signala N.
Također je u praksi česta situacija da je broj uzoraka ograničen prirodom
signala. Primjer takva slučaja je zvuk kojeg proizvodi jedna pritisnuta tipka
klavira.
Posebna je pak situacija kod analize signala kao što su govorni signali.
Govorni signali su nestacionarni slučajni signali zbog čega je računanje
spektra opravdano samo u relativno kratkim intervalima reda 10 ms unutar kojih
se signal može smatrati stacionarnim.
Tri su dakle
glavna razloga zašto se analiza signala temelji na konačnom broju uzoraka:
·
konačna memorija računala
·
signali su ograničena trajanja
·
signal je stacionaran samo u konačnom
intervalu.
Vremensko
ograničenje signala odnosno ograničenje broja uzoraka je od temeljne važnosti
kod razmatranja svojstava DFT.
14.2 Diskretna Fourierova transformacija (DFT)
Neka ![]() predstavlja signal
uzoraka xs(t) ograničen na
N uzoraka (slika 14.1). Vrijedi
dakle:
predstavlja signal
uzoraka xs(t) ograničen na
N uzoraka (slika 14.1). Vrijedi
dakle:
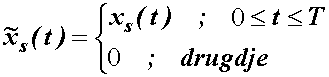
gdje je ![]() .
.
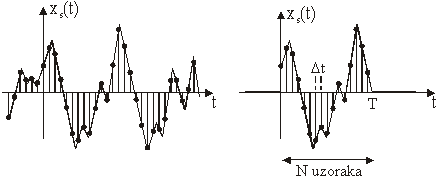
Slika 14.1 Neograničen i ograničen signal uzoraka
Spektralna
gustoća ![]() će općenito
predstavljati samo procjenu spektralne gustoće Xs(f) jer je signal nepoznat izvan intervala [0,T].
će općenito
predstavljati samo procjenu spektralne gustoće Xs(f) jer je signal nepoznat izvan intervala [0,T].
Digitalan
obradnik signala (DSP) računa procjene spektralnih komponenti samo kod
diskretnih vrijednosti frekvencije što znači da DSP 'vidi' ulazni signal kao da
je periodičan s periodom T. Stoga
rezultat DFT nije spektralna gustoća signala ![]() , nego spektralna gustoća periodične funkcije xsp(t)
prikazane na slici 14.2.
, nego spektralna gustoća periodične funkcije xsp(t)
prikazane na slici 14.2.
Vrijedi:
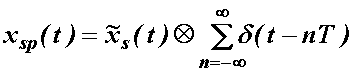 14.1)
14.1)
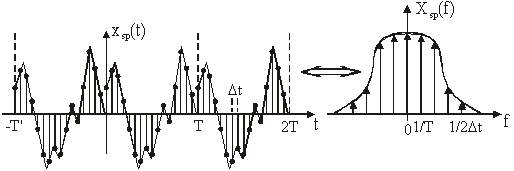
Slika 14.2 Periodičan signal uzoraka i njegova spektralna
gustoća
Kao što je
prikazano na slici 14.2, spektralna gustoća Xsp(f)
je diskretna, što je posljedica digitalne obradbe, ali je i periodična s
periodom ![]() , što je posljedica uzorkovanja (poglavlje
13.2). Naravno,
, što je posljedica uzorkovanja (poglavlje
13.2). Naravno, ![]() treba biti određen u
skladu sa teoremom o uzimanju uzoraka.
treba biti određen u
skladu sa teoremom o uzimanju uzoraka.
Za
periodične signale vrijedi izraz (10.4) tj.:
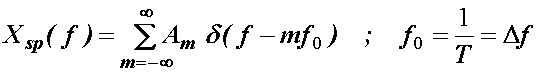 (14.2)
(14.2)
gdje je ![]() rezolucija po
frekvenciji, a Am su kompleksni
rezolucija po
frekvenciji, a Am su kompleksni
Fourierovi
koeficijenti uzorkovanog signala xsp(t).
Kad je to
moguće, T treba birati veći ako se želi u spektru istražiti eventualno prisutnu
finu strukturu.
Za
kontinuirane periodične signale vrijedi (10.8):
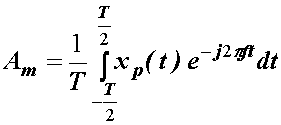 (14.3)
(14.3)
Za signal
uzoraka xsp(t) se može pisati:
![]()
![]()
![]()
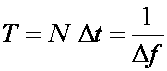
pa (14.3)
postaje:
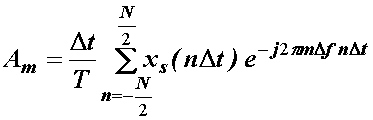
ili:
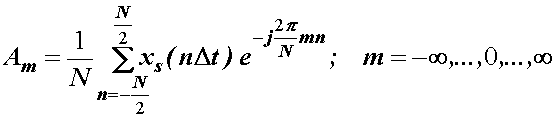 (14.4)
(14.4)
Koeficijenti
Am su periodični s periodom N, pa je za DFT potrebno računati samo N
koeficijenata tako da (14.4) postaje:
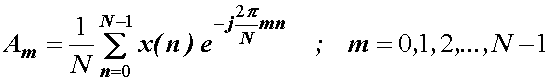 (14.5)
(14.5)
Izraz (14.5)
definira Fourierove koeficijente diskretne Fourierove transformacije
signala x(t). Fourierovi koeficijenti
(14.5) predstavljaju procjenu Fourierovih koeficijenata kontinuiranog signala
x(t) odnosno signala uzoraka xs(t). Pogreška se javlja
zbog konačnog broja uzoraka N, odnosno konačnog vremena snimanja T.
Očigledno će
(14.5) dati točne Fourierove koeficijente samo u slučaju kad je x(t) periodična funkcija sa periodom T
odnosno općenito s periodom T/k ; k = 1,2,3,..., kao što je primjerice
prikazano na slici 14.3.
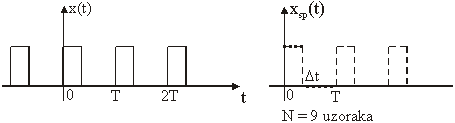
Slika 14.3 Primjer kad DFT daje točan spektar
Ulazni
signal nije općenito periodičan, a ako i jest, njegov period T1 nije
općenito jednak T/k. Stoga je zanimljivo detaljnije razmotriti problem procjene
DFT koeficijenata kao i mogućnost otklanjanja odnosno smanjenja pogreške koja
se javlja u proračunu.
Inverzna
diskretna Fourierova transformacija (IDFT) se u skladu s (10.12) definira
izrazom:
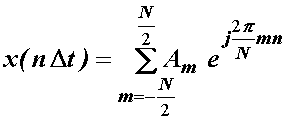 (14.6)
(14.6)
odnosno:
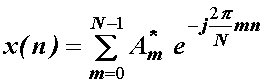 (14.7)
(14.7)
14.3 Učinak propuštanja
Promotrimo
problem ograničenja uzorkovanog signala pri računanju DFT ignorirajući zbog
jednostavnosti činjenicu da je DFT diskretna. Ograničenje signala na interval
T, može se interpretirati kao množenje signala xs(t) sa tzv. prozorskom
funkcijom w0(t) (slika 14.4) gdje je:
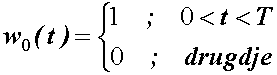 (14.8)
(14.8)
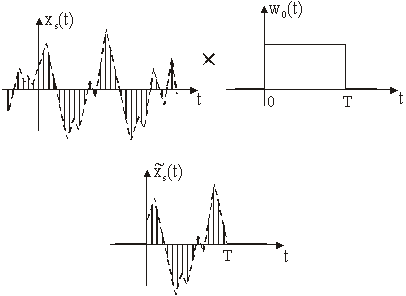
Slika 14.4 Ograničenje signala kao množenje
s prozorskom funkcijom
Množenje
dvaju signala u vremenskom području odgovara konvoluciji njihovih spektralnih
gustoća (izraz 12.31):
![]() (14.9)
(14.9)
Promatrajmo
zbog jednostavnosti samo apsolutne iznose spektralnih gustoća. Spektralna
gustoća w(t) je dana u skladu s
(9.24):
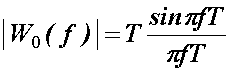 (14.10)
(14.10)
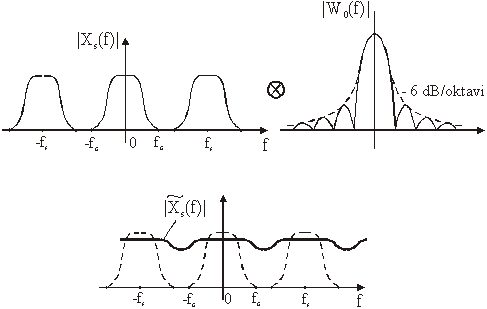
Slika 14.5 Konvolucija spektralnih
gustoća
signala uzoraka i prozora
Slika 14.5
prikazuje rezultirajući spektar ![]() . Zbog konvolucije s W(f) spektar Xsp(f) nije
jednak Xs(f). Općenito uzevši sve su frekvencijske komponente
pogrešne. Nastala se pojava naziva učinak propuštanja. Naime može se reći da je
u postupku računanja DFT došlo do uvlačenja šuma čime je izlazni signal–šum
omjer smanjen. Iz slike 14.6 koja prikazuje spektralnu gustoću se može zaključiti
da je signal-šum omjer samo 13 dB što je za većinu primjena neprihvatljivo
niska vrijednost. Kao posljedica učinka propuštanja javlja se pogreška u
amplitudi DFT koeficijenata od čak 4.4 dB (slika 14.8).
. Zbog konvolucije s W(f) spektar Xsp(f) nije
jednak Xs(f). Općenito uzevši sve su frekvencijske komponente
pogrešne. Nastala se pojava naziva učinak propuštanja. Naime može se reći da je
u postupku računanja DFT došlo do uvlačenja šuma čime je izlazni signal–šum
omjer smanjen. Iz slike 14.6 koja prikazuje spektralnu gustoću se može zaključiti
da je signal-šum omjer samo 13 dB što je za većinu primjena neprihvatljivo
niska vrijednost. Kao posljedica učinka propuštanja javlja se pogreška u
amplitudi DFT koeficijenata od čak 4.4 dB (slika 14.8).
Primjer 14.1 Učinak propuštanja kod DFT sinusnog signala
Promotrimo
sljedeće slučajeve:
·
sinusni signal periodičan u prozoru (T1=T/3)
·
signal neperiodičan u prozoru (T1=T/2.5)
gdje je T1
period signala a T trajanje odnosno širina prozora.
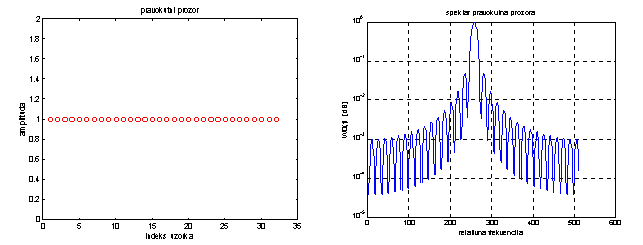
Slika 14.6 Pravokutan prozor i pripadna spektralna gustoća
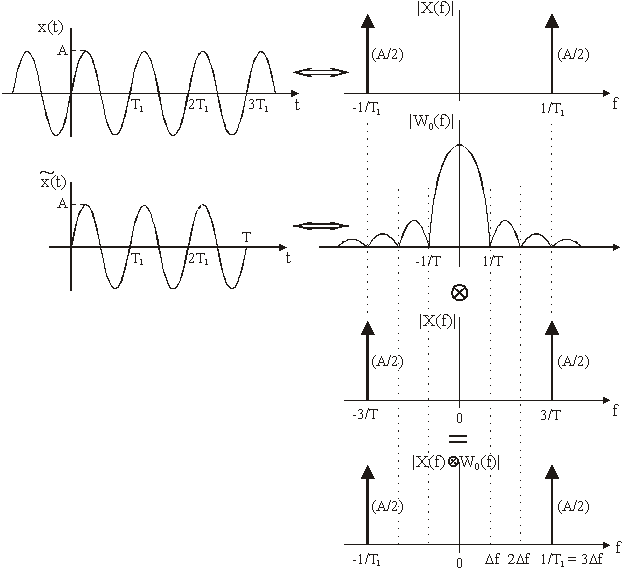
Slika 14.7 DFT sinusnog signala periodičnog u prozoru
(T = 3T1)
Iz slike
14.7 se vidi da u slučaju periodična signala u prozoru (T=3T1),
spektar računat preko DFT je bez greške uz odgovarajuću rezoluciju Df = 1/T.
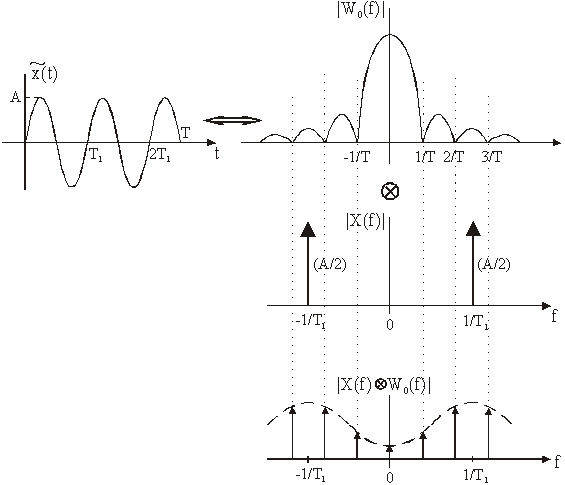
Slika 14.8 DFT sinusnog signala neperiodičnog u
prozoru (T = 2.5T1)
Učinak
propuštanja za slučaj neperiodičnog sinusnog signala u prozoru je očigledan na
slici 14.8. Spektar ![]() sadrži vrlo jak šum tako
da su impulsi kod frekvencija
sadrži vrlo jak šum tako
da su impulsi kod frekvencija ![]() u velikoj mjeri
zamaskirani šumom.
u velikoj mjeri
zamaskirani šumom.
14.4 Optimalne prozorske funkcije
Postavlja se
pitanje kako otkloniti odnosno umanjiti učinak propuštanja.
Očigledno bi
učinak nestao u slučaju kad bi spektralna gustoća prozora imala oblik:
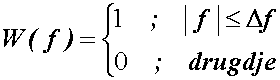 (14.11)
(14.11)
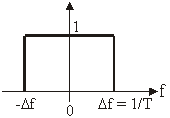
Slika 14.9a Idealan spektar prozora
Uz spektar
prozora kao na slici 14.9a rezultat DFT bi za primjer na slici 14.7 bio jednako
točan. Za slučaj na slici 14.8 rezultat bi bio kao na slici 14.9b.
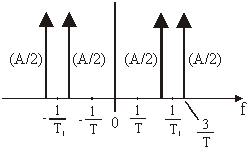
Slika 14.9b DFT uz idealni spektar prozora
Može se reći
da se spektar ![]() na slici 14.9b
podudara sa spektrom Xs(f)
na slici 14.7. Razlika koja
postoji posljedica je konačne rezolucije
na slici 14.9b
podudara sa spektrom Xs(f)
na slici 14.7. Razlika koja
postoji posljedica je konačne rezolucije ![]() .
.
Međutim
pravokutan spektar W(f) na slici
14.9a predstavlja idealizaciju. Vremenska funkcija w(t) ograničena na interval ![]() ne može imati
Fourierovu transformaciju W(f)
ograničenu na interval
ne može imati
Fourierovu transformaciju W(f)
ograničenu na interval ![]() nego je W(f) neograničena.
nego je W(f) neograničena.
Stoga je
potrebno naći prozorsku funkciju w(t)
čija spektralna gustoća najbolje, prema odabranom kriteriju, aproksimira
pravokutni impuls na slici 14.9a. Kriteriji za izbor W(f) mogu biti različiti. Najjednostavniji se kriterij temelji na
energiji u području ![]() . U skladu s tim kriterijem, najpovoljnija W(f) će biti ona kod koje je relativni
udio energije u području
. U skladu s tim kriterijem, najpovoljnija W(f) će biti ona kod koje je relativni
udio energije u području ![]() najveći.
najveći.
Definiramo
energijski omjer:
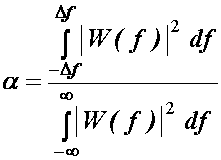 (14.12)
(14.12)
Rješenja
izraza (14.12) koja daju ![]() vode na prozorske
funkcije koje su energijski optimizirane u odabranom području (- k Df, k Df), k =
1,2,3,....
vode na prozorske
funkcije koje su energijski optimizirane u odabranom području (- k Df, k Df), k =
1,2,3,....
Uz područje
integracije od ![]() dobiva se W1(f) koja osigurava najveću
moguću rezoluciju Df = 1/T. U tom slučaju se dobiva
dobiva se W1(f) koja osigurava najveću
moguću rezoluciju Df = 1/T. U tom slučaju se dobiva ![]() tj. glavna latica W1(f) sadrži 98.1% energije
signala.
tj. glavna latica W1(f) sadrži 98.1% energije
signala.
Ako se za
područje integracije uzme ![]() dobiva se W2(f) uz
dobiva se W2(f) uz ![]() .
.
Očito je W2(f) povoljniji sa
stajališta energije, ali treba voditi računa da je uz W2(f) rezolucija
dvostruko niža tj. ![]() . Općenito se može definirati prozor Wk(f) uz rezoluciju kDf.
. Općenito se može definirati prozor Wk(f) uz rezoluciju kDf.
Stvar je određene primjene da li će se birati prozorska funkcija koja ima veći energijski omjer ili prozorska funkcija veće rezolucije.
Slika 14.10
prikazuje ![]() i
i ![]() . Omjer prve najveće sporedne latice i glavne latice može se
smatrati omjerom signal-šum kojeg osigurava dani prozor.
. Omjer prve najveće sporedne latice i glavne latice može se
smatrati omjerom signal-šum kojeg osigurava dani prozor.
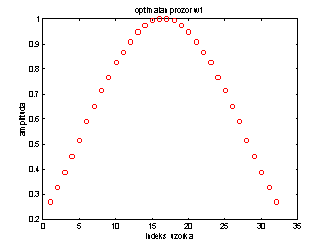
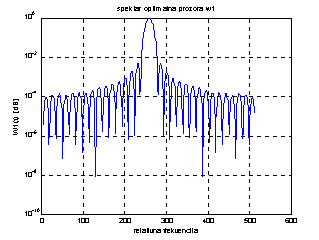
Slika 14.10a Optimalni prozor w1 i pripadna
spektralna gustoća
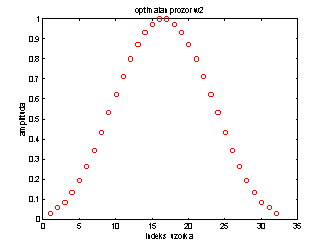
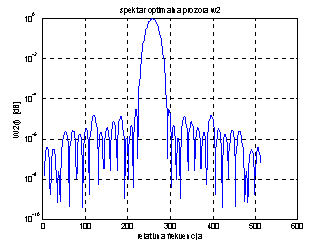
Slika 14.10b
Optimalni prozor w2 i pripadna spektralna gustoća
Slijedi da w1(t) osigurava oko 25 dB, a w2(t) oko 50 dB omjer
signal-šum. Zanimljivo je ove vrijednosti usporediti s 13 dB omjera signal-šum
za pravokutan prozor w0(t)
dan na slici 14.6. Najveća pogreška po amplitudi DFT koeficijenata je kod w1(t) oko 2.2 dB, a za prozor
w2(t) oko 1.2 dB u poredbi
s 4.4 dB za prozor w0(t).
Smanjenje
učinka propuštanja može se postići i sa neoptimalnim prozorskim funkcijama koje
je međutim lako matematički definirati u vremenskom području.
Slika 14.11
prikazuje za primjenu korisne prozorske funkcije i to trokutasti prozor koji se
naziva i Parzenov prozor zatim sinusni prozor. Slika 14.12 prikazuje
prozor podignuti kosinus koji se naziva i Hanning prozor definiran
izrazom:
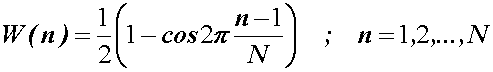
a slika
14.13 prikazuje sličan ali optimalniji prozor pod nazivom Hamming prozor
definiran izrazom:
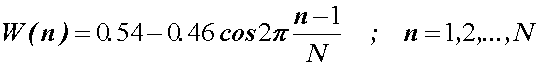
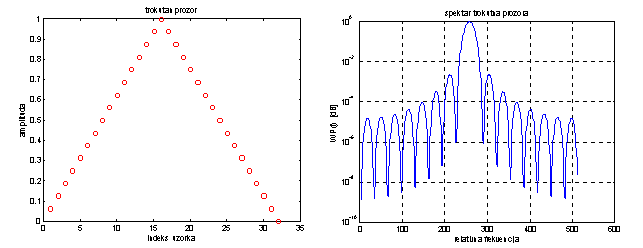
Slika 14.11a Trokutni (Parzenov) prozor i njegova spektralna gustoća
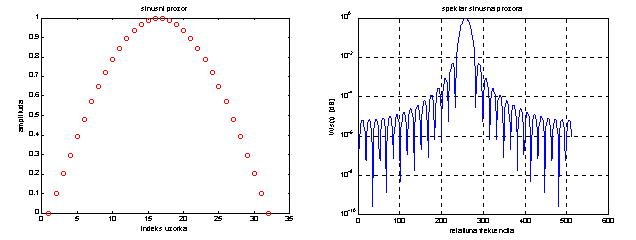
Slika 14.11b Sinusni prozor i njegova spektralna gustoća
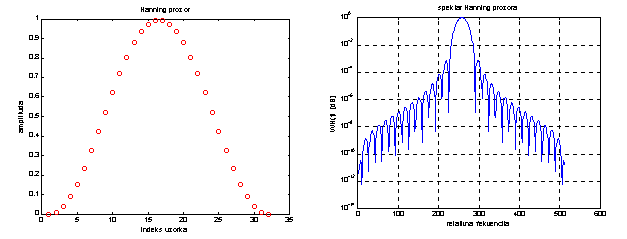
Slika 14.12 Hanning prozor i njegova spektralna gustoća
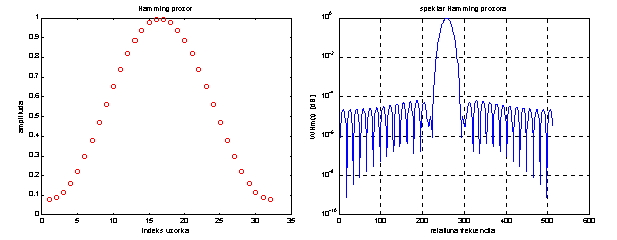
Slika 14.13 Hamming prozor i njegova spektralna gustoća
Hannov
prozor je vrlo blizak prozoru w2(t)
koji je dobiven maksimiziranjem energijskog omjera (14.12). Ovaj prozor se može
primijeniti izravno u frekvencijskom području putem izraza:
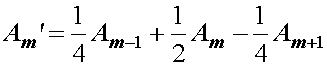 (14.16)
(14.16)
gdje su Am'
modificirani Fourierovi koeficijenti s umanjenim učinkom propuštanja.
Među
mnogobrojnim tipovima prozorskih funkcija, spomenimo još one koje se temelje na
ograničenju razine sporednih latica u Fourierovoj transformaciji uz minimalnu
širinu glavne latice. Dobiveni prozori se nazivaju i Dolph-Chebyshevljevi
filtri. Slika 14.14 prikazuje primjer takva prozora u vremenskom i
frekvencijskom području dobiven uz razinu sporednih latica od – 60 dB.
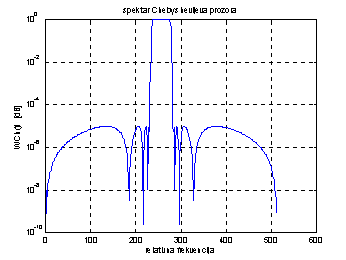
Slika 14.14 Spektralna gustoća Dolph-Chebyshevljeva prozora
Primjer Dolph-Chebyshevljeva
prozora na slici 14.14 ima razinu šuma – 60 dB i najveću pogrešku u amplitudi
DFT koeficijenata od 0.75 dB.
Zaključak
Uporaba optimalnih prozorskih funkcija koje umanjuju
učinak propuštanja je standardan postupak kod računanja DFT. Slika 14.15
prikazuje shemu koja uključuje množenje signala s prozorskom funkcijom.
Digitalni analizatori spektra sadrže izbornik prozorskih funkcija koje se
biraju tako da se maksimizira točnost ili maksimizira rezolucija.
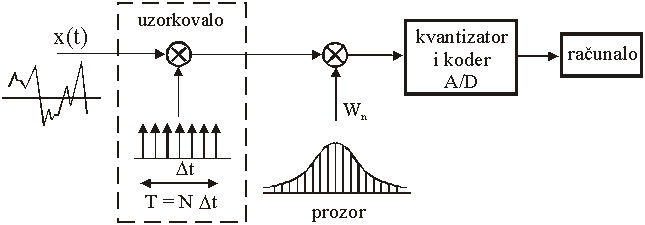
Slika 14.15 Blok shema DFT analize