14.5 BRZA FOURIEROVA TRANSFORMACIJA (FFT)

Izraz (14.5) za DFT:

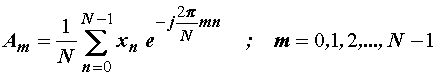
može se pisati u obliku:

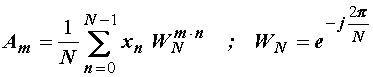(14.16)

gdje je W_N tzv. rotacijski faktor.

Izraz (14.16) u matričnom obliku je:

A=W x (14.17)

gdje su A i x N-dimenzionalni vektori a W je kvadratna N´N matrica.

Rješenje gornje matrične jednadžbe zahtijeva kompleksnih množenja i zbrajanja. Vrijedi dakle

(14.18)

Za velike N (N > 50), vrijeme računanja i potrebna memorija su značajni.

Može se općenito uzeti da svaki računski postupak čija složenost raste s potencijom od N nije za primjene prikladan posebice za relativno veliki N. Štoviše, zbog velikog broja množenja i zbrajanja, može se računati s relativno velikom pogreškom odnosno šumom zaokruživanja.

FFT algoritam (J.W.Cooley i J.W.Tukey 1965.)

Niz se uzoraka dijeli u dvije grupe od po N/2 uzoraka. Podjela se temelji na parnim i neparnim indeksima tj. prvi dio čine x₀, x₂, x₄,... a drugi dio čine x₁, x₃, x₅,... (slika 14.16). Vrijedi dakle:

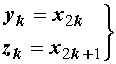
(14.18)

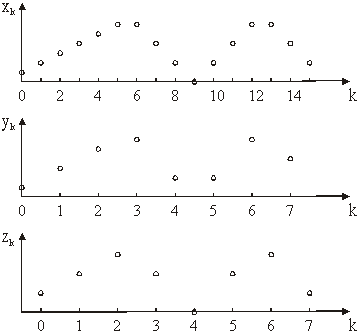
Slika 14.16 Originalni niz x_n i podnizovi y_k i z_k

DFT za nove nizove od po N/2 uzoraka slijedi iz (14.16):

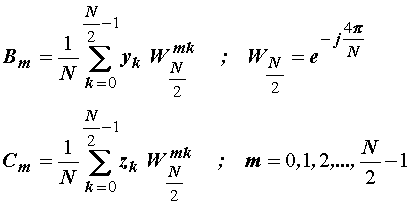(14.19)

Potrebno je naći relaciju koja povezuje koeficijente A_m sa B_m i C_m koeficijentima. Vrijedi:

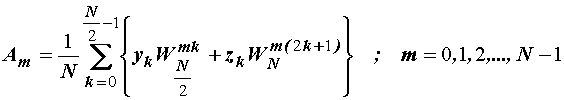
ili:

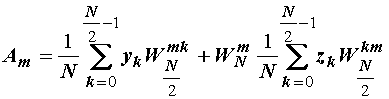(14.20)

Izraz (14.20) uz izraz (14.19) postaje:

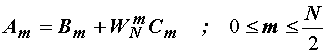(14.21)

Za 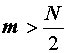, Fourierovi koeficijenti B_m i C_m se ponavljaju simetrično. Zamjena sa 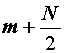u (14.21) daje:

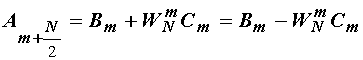(14.22)

jer vrijedi: .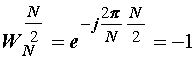

Iz (14.21) i (14.22) slijedi:

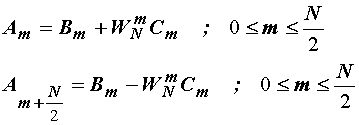(14.23)

Izraz (14.23) kaže da se N Fourierovih koeficijenata vremenskog niza x_n (n=0,1,..., N-1) može dobiti preko N/2 Fourierovih koeficijenata dobivenih preko dvije DFT sa po N/2 uzoraka (slika 14.17).

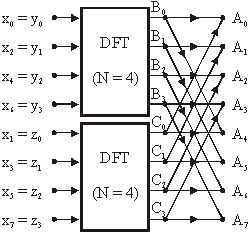
Slika 14.17 DFT od N = 8 uzoraka izražena putem

dvije DFT od N/2 uzoraka

Na isti se način, dijeljenjem nizova y_k i z_k na po dva dijela, DFT svakog od ovih nizova tj. 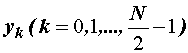i 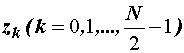može računati putem dvije DFT od N/4 uzoraka. Slika 4.18 prikazuje primjer kako se DFT od 8 uzoraka računa putem četiri DFT od po dva uzorka.

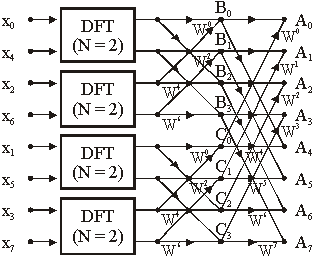
Slika 14.18 DFT od N = 8 uzoraka izražena

putem četiri DFT od N/4 uzoraka

Navedeni način dijeljenja se primjenjuje toliko puta dok se na kraju ne dobije N puta DFT od po samo jednog uzorka gdje je naravno DFT jednog uzorka jednaka samom uzorku. Za primjer N = 8 slika 14.19 prikazuje dijagram toka računanja svih N Fourierovih koeficijenata.

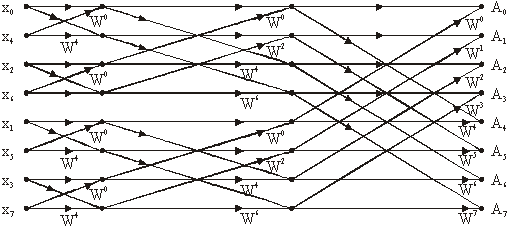
Slika 14.19 Dijagram toka FFT postupka za N = 8

Očigledno je opisani postupak računanja vrijedi samo uz uvjet:

Dakle, broj uzoraka vremenskog niza x_n treba imati neku od vrijednosti:

N=2,4,8,...,128,256,512,...,4096,...

Međutim, moguće je, uz određenu modifikaciju, koristiti opisani FFT algoritam i za bilo koji N (tj. ).

Iz dijagrama toka na slici 14.19 slijedi da je potrebno preuređenje redosljeda ulaznih uzoraka. Međutim preuređenje redosljeda ulaznih uzoraka je obično neprihvatljivo posebice kod obrade signala u stvarnom vremenu. Problem redoslijeda ulaznih uzoraka se može riješiti pretvorbom dijagrama na slici 14.19 u oblik kao na slici 14.20.

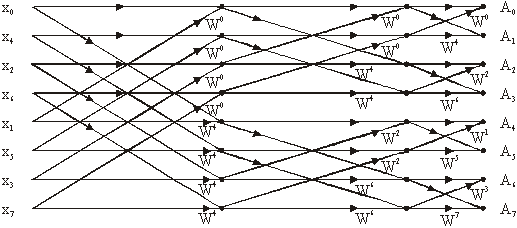
Slika 14.20 FFT dijagram toka s pravilnim

redoslijedom ulaznih uzoraka

Na slici 14.20 je očigledno pomiješan redosljed Fourierovih koeficijenata. Ako se redoslijed označi binarnim kodom(slika 14.21) može se lako uočiti da se radi o zrcaljenom redosljedu po bitima.

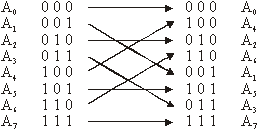
Slika 14.21 Preuređenje redosljeda Fourierovih

koeficijenata uz N = 8

Preuređenje redosljeda Fourierovih koeficijenata je obično sastavni dio FFT podprograma koji se standardno koriste u različitim programskim paketima (npr. Matlab).

Iz dijagrama toka za FFT slijedi da se cijelokupan proračun izvršava u M = ld N koraka. Također je očigledno da jednom uzeta vrijednost uzorka, odnosno izračunata međuvrijednost, nije više potrebna u daljnjim koracima pa ona može ustupiti mjesto novoj izračunatoj vrijednosti. Tako se na jednom mjestu u memoriji, u kojoj je na početku pohranjena jedna kompleksna vrijednost uzorka, smjenjuje M vrijednosti tijekom cijelog FFT računa da bi se na kraju pohranila kompleksna vrijednost Fourierovog koeficijenta. Očito je za FFT algoritam potrebno samo N kompleksnih mjesta u memoriji računala.

Može se dakle zaključiti da je vrijeme računanja FFT razmjerno s , dakle vrijedi:

(14.24)

Primjer: Neka je N = 2¹⁰ = 1024 pa iz (14.18) i (14.24) slijedi:

Dakle uz N = 1024, FFT proračun se izvršava oko 100 puta brže od DFT proračuna.

Faktor ubrzanja je tim veći što je veći N. Slika 14.22 prikazuje faktor ubrzanja FFT u odnosu na DFT za . Uz N = 2²⁰ FFT se izvodi oko 50000 puta brže od DFT.

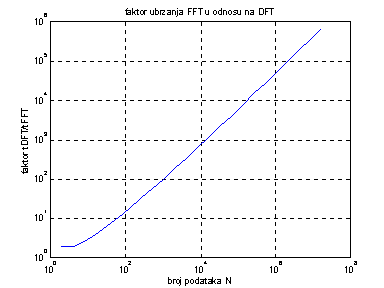
Slika 14.22 Faktor ubrzanja proračuna FFT

u odnosu na DFT

14.6 Primjene FFT

Primjena FFT je vrlo široka. Područja primjene su primjerice kod analize glasova, analize vibracija mehaničkih konstrukcija, analize seizmograma, analize kardiograma i moždanih valova, određivanje prijenosne funkcije sustava, računanje korelacije i konvolucije, digitalno filtriranje, kodiranje audio i video signala i brojna druga.

Slika 14.23 ilustrira analizu vibracija krila zrakoplova koji nosi dva pogonska motora s propelerima, a slika 14.24 prikazuje analizu moždanih signala (elektroencefalograma). Slika 14.25 prikazuje analizu glasova, slika 14.26 prikazuje analizu podzemnih signala kod istraživanja plina i nafte, a slika 14.27 prikazuje određivanje prijenosne funkcije mehaničkog sustava mjerenjem odziva na impuls. Većina spomenutih primjera se temelji na računanju diskretne autokorelacije i korelacije putem FFT.

Slika 14.23 Analiza vibracija krila zrakoplova

Slika 14.24 Analiza moždanih valova (elektroencefalografija)

Spektogram glasa

Slika 14.25 Analiza glasova

14.7 Računanje diskretne korelacije i konvolucije pomoću FFT (CDK)

Promotrimo diskretnu konvoluciju. Za vremenske nizove x_n i h_n, konvolucija je dana izrazom koji slijedi iz (12.23):

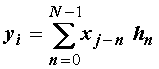(14.25)

ili:

y = X h

gdje je X kvadratna N´N matrica.

Slično računanju DFT vrijeme računanja je i ovdje razmjerno s N². Za velike je N, proračun putem FFT (slika 14.28) povoljniji.

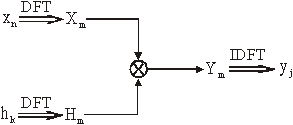
Slika 14.28 Proračun konvolucije putem DFT odnosno FFT

Izlazni niz y_j je prema slici 14.23 uz (14.16) dan izrazom:

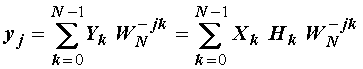
gdje je .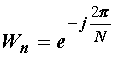

Ako se X_k i H_k izraze kao DFT nizovi x_n i h_k slijedi:

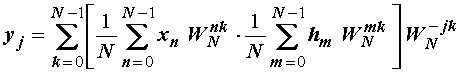
ili:

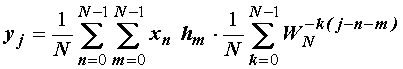(14.26)

Budući vrijedi:

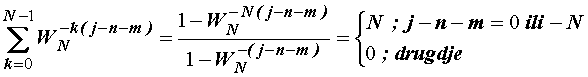
Zbrajanje po m u izrazu (14.26) daje:

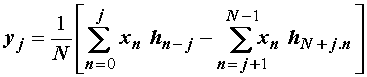(14.27)

Drugi član na desnoj strani (14.27) predstavlja ciklični član pa izraz (14.27) predstavlja tzv. cikličnu diskretnu konvoluciju (CDK). Cikličnost je posljedica periodičnih nizova x_n i h_k, kakve ih uzima DFT.

Zaključak: Vrijednosti konvolucije y_j, računate preko CDK (14.27) su točne samo u slučaju kad su x_n i h_k periodični nizovi s periodom N.

Takav primjer gdje su nizovi x_n i h_n periodični i jednakog perioda N prikazuje slika 14.29.

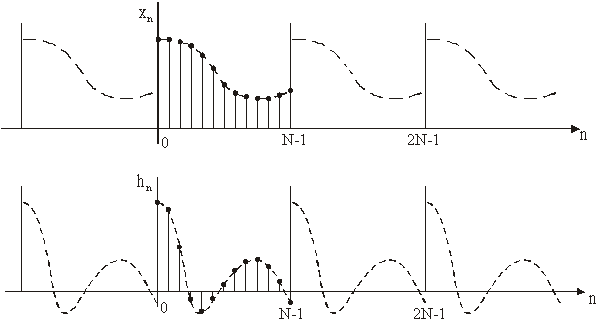
Slika 14.29 Primjer periodičnih diskretnih nizova x_n i h_n

Slika 14.28 predstavlja međutim samo specijalan slučaj. Općenito nizovi x_n i h_n nisu periodični. Općenito su moguće sljedeće situacije:

a) nizovi x_n i h_n su konačni

b) niz h_n je konačan, x_n neograničen

c) oba niza su neograničena.

Pod neograničenim se vremenskim nizom podrazumijeva vrlo dug niz tako da ga nije moguće odjednom u cjelini uzeti u račun.

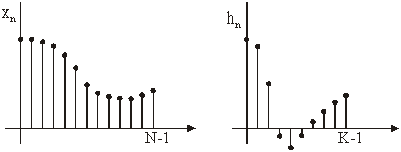
Slika 14.30 Konačni nizovi x_n i h_n dužina N i K

Proračun CDK putem izraza (14.27) zahtijeva definiciju sljedećih nizova:

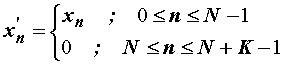
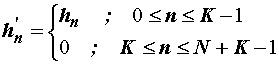(14.28)

pa izraz (14.27) poprima oblik:

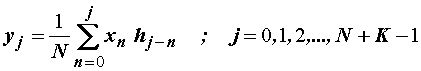
jer je doprinos cikličnog člana uz (14.28) jednak nuli.

Periodični nizovi x_np i h_np stvarno su definirani samo u području (0, N+K-1), a DFT odnosno FFT ih uzima periodičnim (slika 14.31).

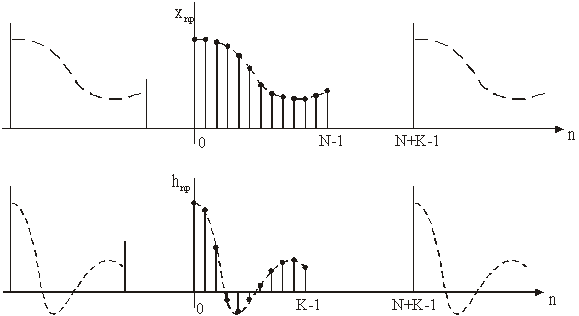
Slika 14.31 Nizovi definirani izrazom (14.28)

kakvim ih uzima DFT

Jedan od nizova je neograničen. Slika 14.32 prikazuje ovu situaciju

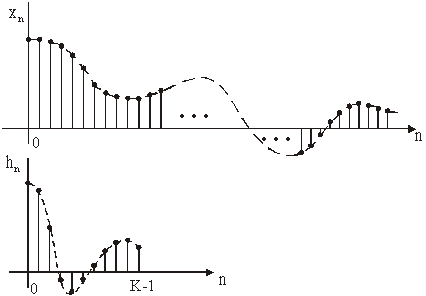
Slika 14.32 Primjer 'neograničena' i ograničena niza

koja je tipična u slučaju kad x_n predstavlja ulaz a h_n predstavlja odziv stabilna linearna sustava (poglavlje 15). Za odziv stabilna sustava možemo praktički uzeti da je jednak nuli za . U slučaju kad niz x_n ima N vrijednosti, i vrijedi N>K, nizu h_n treba dodati nule do N-1 vrijednosti (slika 14.33).

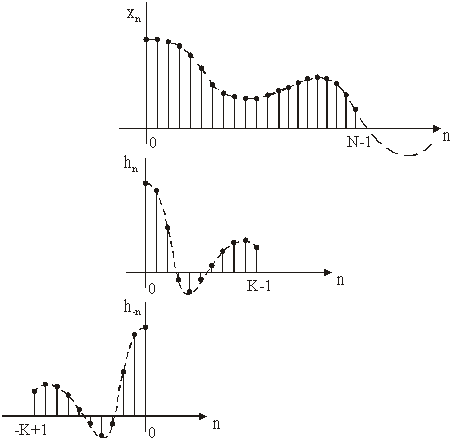
Slika 14.33 Konvolucija neograničena i ograničena niza

Može se uočiti iz izraza (14.27) da su u ovom slučaju kao što je prikazano na slici 14.34 točne samo vrijednosti konvolucije u intervalu (K , N - 1).

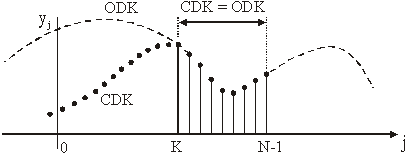
Slika 14.34 Rezultat proračuna CDK za nizove

na slici 14.32 na temelju (14.27)

Može se dakle pisati:

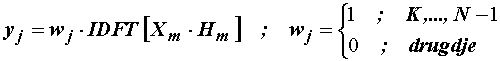
Kako dobiti preostale točke konvolucije? Prvih K vrijednosti mogu biti dobivene tako da se niz x_n pomakne u desno za K mjesta, pa se prvih K vrijednosti uzme jednake nuli. Segment niza x_n je sada uzet u dužini N = L + K – 1 kao na slici 14.35.

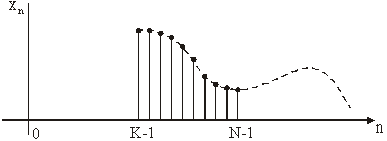
Slika 14.35 Novi segment niza x_n dužine N

U prvom koraku, CDK će onda dati točne vrijednosti u intervalu (K , N - 1). Ovih N -K +1 vrijednosti cirkularne konvolucije odgovara prvim vrijednostima prave konvolucije, dakle:

Za dobivanje ostalih vrijednosti treba uzeti sljedećih N vrijednosti niza x_n, od N-K+1 do 2(N-K+1) i tranzlatirati ih u niz u intervalu (0,N-1), pa CDK daje točne vrijednosti u intervalu (K,N-1). Izračunate vrijednosti treba tranzlatirati na već dobiveni dio niza (0,N-K+1). Time su dobivene vrijednosti konvolucije u intervalu (0,2(N-K+1)). Postupak se nastavlja. Slika 14.36 ilustrira opisani postupak.

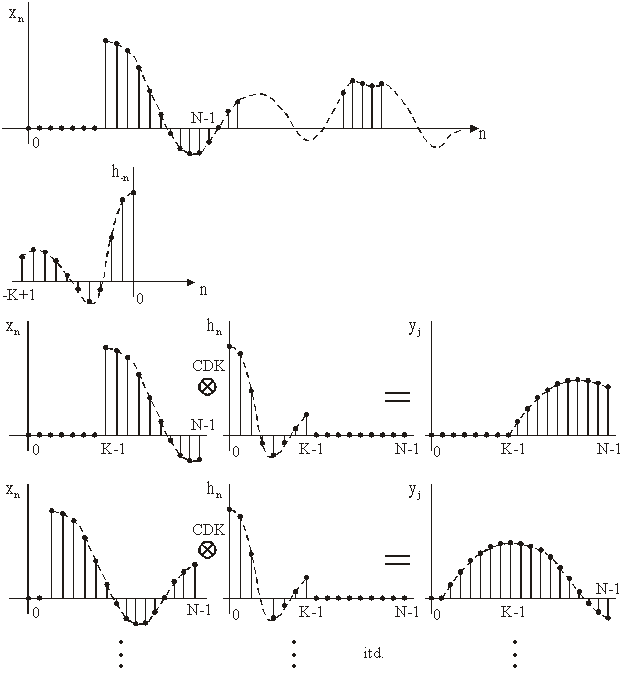
Slika 14.36 Prikaz računanja konvolucije

putem (14.27) korak po korak

Nizanjem svih točnih vrijednosti dobiva se svih L željenih točaka CDK (slika 14.37).

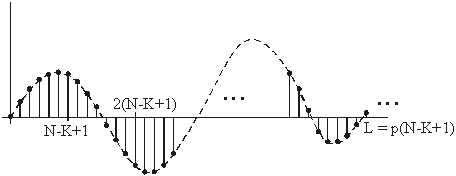
Slika 14.37 Konvolucija izračunata u području

(0 , L = p(N – K + 1)) uz p = 1,2,...

Računanje diskretne autokorelacije i korelacije je slično računanju diskretne konvolucije uz jedinu razliku što u frekvencijskom području treba uzeti kompleksno konjugiranu Posebno je jednostavno računanje autokorelacije. Neka je niz x_n definiran u području (0, N-1) i neka je potrebno odrediti autokorelaciju u K točaka. Obično je broj željenih vrijednosti autokorelacije relativno malen (K<<N), pa se vrijednosti autokorelacije u području (0,K) mogu izračunati dodavanjem K nula na kraj niza kao što je prikazano na slici 14.39.

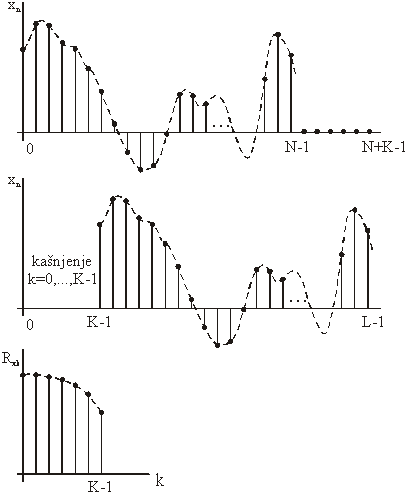
Slika 14.39 Ilustracija za proračun diskretne autokorelacije

Vrijedi:

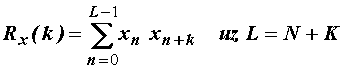
Npr. ako je poznat niz od 836 uzoraka za koji treba odrediti autokorelaciju za kašnjenje od 0 do 100, razumno je na kraj niza dodati 178 nula tako da je L=836+178=1024 što je prikladno za primjenu FFT algoritma uz M = 10 tj. 2¹⁰ = 1024.