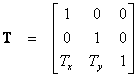
*Napomena: ovo su primjeri mogucih
pitanja koja studenti mogu koristiti pri pripremi za ispite za samostalnu provjeru znanja.
1. Objasnite značenje pojma homogenih koordinata.
Homogena predstava objekta u n-dimenzionalnom prostoru je objekt u (n+1)-dimenzionalnom prostoru. Radi se o nejednoznačnom preslikavanju jer postoji beskonačno mnogo ekvivalentnih predstava objekta iz n-dimenzionalnog prostora u (n+1)-dimenzionalnom prostoru (preslikavanje jednog u mnogo). Vrijednost dodatne koordinate može se proizvoljno odabrati (npr. može imati smisao faktora proporcionalnosti). Inverzno preslikavanje naziva se projekcija (preslikavanje mnogo u jedno). Homogena predstava točke u 2D prostoru (x,y) je homogena točka (x1,x2,x3).
2. Opišite postupak transformacije točke u 3D prostoru.
Ako je općenita transformacija homogene točke u 3D prostoru definirana matricom M tada se njena transformacija može opisati na sljedeći način:
1. homogena predstava točke (x,y,z) u homogenom prostoru je homogena točka (x1,x2,x3,x4)
2. koordinate točke transformirane homogene točke [x’1 x’2 x’3 x’4 ] određene su sljedećom jednadžbom
[x’1 x’2 x’3 x’4 ] = [x1 x2 x3 x4 ] M
Transformacija objekta obavlja se tako da se ista transformacija primijeni na sve njegove točke.
3. Napišite matricu translacije koja definira pomak za 3 ulijevo u horizontalnom smjeru i za 5 u vertikalnom smjeru.
Tx = -3
Ty = 5
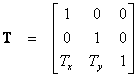
4. Napišite matricu rotacije koja definira zakret točke oko ishodišta za kut od 60° u smjeru suprotnom od kazaljke na satu.
Θ = 60°
cos Θ = 0.5
sin Θ = 0.86
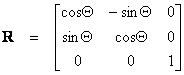
5. Koje su osnovne značajke i vrste ravninskih geometrijskih projekcija?*
Ravninske geometrijske projekcije se u načelu odvijaju na način da projekcijske zrake koje izlaze iz projekcijskog središta prolaze kroz sve točke objekta i presjecaju projekcijsku ravninu tvoreći u njoj oblik projekcije. Postoji više vrsta ravninskih geometrijskih projekcija koje su prikladne za različite namjene, a osnovne dvije skupine su perspektivne projekcije i paralelne projekcije. Temeljna razlika je u odnosu projekcijskog središta i projekcijske ravnine. Kod paralelnih projekcija udaljenost projekcijskog središta i projekcijske ravnine je beskonačna, dok je kod perspektivnih projekcija ta udaljenost beskonačna.
6. Na koji način se matematički definira ortogonalna projekcija na xy ravninu?*
Ortogonalna projekcija na xy-ravninu odgovara odabiru konstantne vrijednosti z koordinate iznosa 0 tj. z=0. Matematički se ova operacija može definirati kao množenje vektora s dijagonalnom matricom čiji su svi elementi jednaki jedinici osim trećeg koji je jednak nuli.
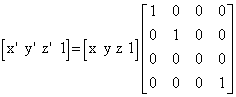
7. Koja je osnovna značajka perspektivne projekcije i kako se ona matematički može definirati?*
Kod perspektivne ili fotografske projekcije projekcijske zrake izviru iz jedne točke na konačnoj udaljenosti od projekcijske ravnine. Ako se promatrač se nalazi na udaljenosti h od projekcijske ravnine perspektivna projekcija se može matematički definirati na sljedeći način:

8. Od kojih se koraka sastoji osnovni inkrementalni algoritam za cratnje ravnih crta?
Osnovni inkrementalni algoritam se sastoji od sljedećih koraka:
· proračun nagiba pravca m = Dy/Dx (|m| < 1),
· proračun nove vrijednosti xi povećanjem prethodne vrijednosti za 1,
· proračun vrijednosti yi = m xi + B,
· isticanje piksela (xi, Round(yi)) gdje je Round (yi) = Floor (0.5 + yi).
9. Na koji način se izbjegava operacija množenja u digitanom diferencijalnom analizatoru?*
Množenje se može izbjeći ako se izraz za proračun vrijednosti koordinate y u eksplicitnom obliku jednadžbe pravca napiše na sljedeći način:
yi+1 = m xi+1 + B = m (xi+Dx) + B = yi + m Dx
Uz izbor Dx = 1 slijedi yi+1 = yi + m.
10. Na sažet način opišite način izbora sljedeće točke pri crtanju ravne crte primjenom algoritma središnje točke?*
Pretpostavimo da je posljednja odabrana točka P s koordinatama (xp,yp) te da je potrebno odabrati sljedeću desnu točku. Odabir se svodi na izbor između dviju mogućih točaka: susjedne točke D do koje se dolazi pomakom udesno za jedan i točke GD do koje se dolazi pomakom za jedan udesno i za jedan prema gore. Potrebno je odrediti koja od te dvije točke je bliža idealnom pravcu. Označimo s T točku sjecišta idealnog pravca s dužinom koja povezuje točke D i GD. Izbor sljedeće točke svodi se na određivanje kojoj je od te dvije točke bliža točka T. Prvo se definira središnja točka S(xp+1, yp+1/2) kao točka polovišta dužine koja povezuje točke D i GD. Odluka se donosi na temelju informacije o položaju središnje točke u odnosu na idealni pravac. Ako je središnja točka S ispod idealnog pravca onda je očito točka GD bliža idealnom pravcu. Ako je središnja točka S iznad središnje točke onda je točka D bliža idealnom pravcu.
11. Kako se odvija postupak izbora piksela pri ispunjavanju likova?
Izbor piksela koje treba ispuniti odvija se u sljedećim koracima:
· skaniranje po horizontalnim crtama (retcima piksela),
· proračun presjecišta horizontalne i primitivnog oblika inkrementalnim algoritmom (odabiru se točke koje leže unutar oblika),
· poredavanje presjecišta po veličini x koordinate,
· ispunjavanje odsječaka koji leže unutar primitivnog oblika (između neparnih i parnih presjecišta).
12. Zašto su u računarskoj grafici posebno zanimljive aproksimacije krivulja trećeg reda?
Za visoku razinu podudarnosti linearnog aproksimacijskog modela i željene krivulje potreban je velik broj linearnih segmenata. Veća razina podudarnosti odnosno bolja aproksimacija uz manji broj pojedinačnih segmenata može se ostvariti primjenom aproksimacija višeg reda. Na taj način smanjuje se potrebna količina memorije i olakšava interaktivni rad pri modeliranju. Najčešće se koriste aproksimacije trećeg reda jer aproksimacije nižeg reda ne daju dovoljno fleksibilnosti za oblikovanje različitih krivulje, a aproksimacije višeg reda su računski zahtjevnije i složenije za primjenu.
13. Na koji način se definira model krivulje primjenom parametarskih krivulja trećeg reda?
Q(t) = [x(t) y(t) z(t)]
gdje je
x(t) = ax t3 + bx t2 + cx t + dx
y(t) = ay t3 + by t2 + cy t + dy
z(t) = az t3 + bz t2 + cz t + dz
uz 0 £ t £ 1.
Ako definiramo vektor potencija parametra t na sljedeći način:
T = [ t3 t2 t 1]
te matricu koeficijenata triju polinoma na sljedeći način:
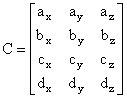
tada možemo pisati izraz za model odsječka krivulje u sažetom obliku
Q(t) = T C.
*14. Definirajte pojam geometrijskog kontinuiteta.
Geometrijski kontinuitet G0 odgovara svojstvu neprekinutosti krivulje u točki dodira dvaju odsječaka. Geometrijski kontinuitet G1 odgovara svojstvu jednakosti vektora smjera tangente u točki dodira dvaju odsječaka.
*15. Definirajte pojam parametarskog kontinuiteta.
16. Navedite tri vrste parametarskih krivulja trećeg reda i pripadne geometrijske uvjete.
S obzirom na izbor vrste geometrijskih uvjeta definirane su različite vrste krivulja. Osnovne vrste krivulja su:
· Hermiteove krivulje (uvjeti su: dvije krajnje točke i dva vektora smjera u krajnjim točkama),
· Bezierove krivulje (uvjeti su: dvije krajnje točke i dvije dodatne točke koje određuju vektroe smjera u krajnjim točkama),
· B-krivulje i b-krivulje (uvjeti su: četiri kontrolne točke).
17. Na koji način se mogu pretvarati parametarske krivulje s jednom baznom matricom u parametarske krivulje s drugom baznom matricom?
Sve skupine krivulja predstavljene matričnim umnoškom Q(t)=TMG moguće je međusobno pretvarati iz jednih u druge npr. krivulje predstavljenu baznom matricom M1 i geometrijskim vektorom G1 moguće je predstaviti drugom baznom maticom M2 i odgovarajućim geometrijskim vektorom G2. Važno je da mora biti ispunjen uvjet:
M2 G2= M1 G1
Nepoznati geometrijski vektor G2 može se izračunati na sljedeći način:
G2 = M2-1M1 G1
18. Na temelju kojih kriterija se odabire vrsta parametarskih krivulja trećeg reda?
Kriteriji za izbor vrste krivulje uključuju:
· prikladnost za interaktivnu manipulaciju,
· stupanj kontinuiteta,
· općenitost,
· brzinu proračuna.
19. Kojim geometrijskim uvjetima su definirane Bezierove krivulje?
Bezierove krivulje definirane su sljedećim geometrijskim uvjetima:
· dvije krajnje točke P1 i P4.
· dvije kontrolne točke P2 i P3 koje određuju vektore smjera u krajnjim točkama R1 i R4.
Pomoću dviju kontrolnih točaka posredno su definirani vektori smjera tangenti R1 i R4 u dvjema krajnjim točkama. Vektor smjera tangente u početnoj točci odgovara derivaciji krivulje Q(t) za vrijednost parametra t=0, dok vektor smjera tangente u krajnjoj točci odgovara derivaciji krivulje Q(t) za vrijednost parametra t=1.
20. Koji su uvjeti kontinuiteta prvog reda za Bezierove krivulje?
Uvjet za G1 kontinuitet jest da točke P3, P4 i P5 moraju biti različite i kolinearne
P3 - P4 = k (P4 - P5), k > 0
Uvjet za C1 kontinuitet jest da je k = 1.
*21. Na koji način se odvija iterativni proračun za crtanje parametarskih krivulja?
Iterativni proračun odvija se na način da se vrijednosti koordinanata x(t), y(t), i z(t) pojedinih točaka izračunavaju za niz vrijednosti parametra t međusobno udaljenih za unaprijed određeni konstantan iznos d. Proračunate točke spajaju se ravnim crtama. Problem ovakvog pristupa je u tome što se unaprijed treba odrediti razmak točaka s obzirom na parametar t. Prevelik razmak rezultira slabom kvalitetom aproksimacije dok premalen razmak rezultira nepotrebnim proračunskim opterećenjem.
*22. Na koji način se odvija rekurzivna podjela za crtanje parametarskih krivulja?
Rekurzivna podjela odvija se na način da se između svake dvije izračunate točke umeće treća točka. Rekurzivna podjela zaustavlja se adaptivno kada odsječak krivulje postane dovoljno ravan da se može aproksimirati ravnom crtom. Pojedinosti postupka različite su za pojedine vrste krivulja. Ovaj pristup je posebice prikladan za Bezierove krivulje. Prednost ovog pristupa je u tome što se izbjegavaju nepotrebni proračuni, a nedostatak je što se mora ispitivati ravnoća pojedinih dijelova.
23. Navedite najčešće korištene načine modeliranja površina u trodimenzionalnom prostoru.*
Najčešće korišteni načini modeliranja površina u trodimenzionalnom prostoru temelje se na primjeni:
· parametarskih površina,
· mreža višekuta,
· površina drugog reda.
24. Kako se definiraju Bezierove površine trećeg reda?*
Ako u općem izrazu za dvoparametarsku krivulju trećeg reda uvrstimo Bezierovu baznu matricu MB i Bezierovu geometrijsku matricu GB dobivamo izraze za Bezierove površine:
![]()
![]()
![]()
Bezierova geometrijska matrica sastoji se od 16 kontrolnih točaka.
25. Kako se odvija iterativni postupak crtanja dvoparametarskih krivulja trećeg reda?*
Iterativni postupak podrazumijeva proračun polinoma trećeg reda za niz bliskih rastućih vrijednosti parametara t i s. Mogući pristup je iscrtavanje niza krivulja kao funkcija parametra t (dok se vrijednost parametra s drži konstantnom za pojedinu krivulju, a mijenja se od krivulje do krivulje). Zatim se iscrtava niz krivulja kao funkcija parametra s (dok se vrijednost parametra t drži konstantnom za pojedinu krivulju, a mijenja se od krivulje do krivulje).
26. Kako se odvija rekurzivni postupak crtanja dvoparametarskih površina trećeg reda?*
Postupak rekurzivne podjele podrazumijeva dijeljenje površine na četverokute (omeđene krivuljama) do zadovoljavajuće ravnoće rezultirajućih četverokuta. Podjela se obavlja dijeljenjem prvo po jednom, a zatim po drugom parametru. Dijeljenje se obavlja crtanjem krivulje po jednom parametru uz konstantnu vrijednost drugog parametra. Konstantna vrijednost drugog parametra određuje se kao aritmetička sredina između vrijednosti tog parametra koje su korištene u prethodnoj podjeli.
27. Što je mreža višekuta?*
Mreža višekuta je skup bridova, vrhova i višekuta povezanih tako da oblikuju površinu koja dovoljno dobro aproksimira željenu površinu. Pri tome svaki brid zajednički je za najviše dva višekuta, a svaki vrh zajednički je za najmanje dva brida. Svaki brid povezuje dva vrha. Višekut je zatvoreni skup povezanih bridova (stranica). Postoji više načina za definiranje podataka o mreži višekuta, a temeljna razlika je u odnosu prema dva međusobno suprotstavljena kriterija: minimizaciji memorijskih zahtjeva i minimizaciji računske složenosti.
28. Koje su značajke eksplicitnog prikaza mreže višekuta?*
U eksplicitnom prikazu svaki je višekut predstavljen listom koordinata vrhova:
P = ((x1, y1, z1), (x2, y2, z2), ...,(xn, yn, zn))
Vrhovi su u ovom prikazu poredani redom iscrtavanja. Nedostatak ovog pristupa je u tome što se vrhovi pojavljuju više puta jer ne postoji eksplicitna predstava zajedničkih vrhova. Npr. za pomicanje (npr. pomoću miša) jednog vrha nužno je identificirati sve višekute povezane s tim vrhom. U tu svrhu nužno je usporediti sve koordinate vrhova u jednom višekutu s koordinatama vrhova u svim drugim višekutima. Pored toga i svi zajednički bridovi se iscrtavaju dva puta.
29. Koje su značajke prikaza mreže višekuta temeljenog na strukturi pokazivača na listu vrhova?*
U prikazu temeljenom na strukturi pokazivača na listu vrhova svaki vrh se pohranjuje samo jednom u listu vrhova
V = ((x1, y1, z1), (x2, y2, z2), ...,(xn, yn, zn))
Višekut se definira listom pokazivača (indeksa) u listu vrhova. Memorijski zahtjevi su znatno manji nego u eksplicitnom prikazu. Osim toga i promjena koordinata jednog vrha je jednostavna jer nije potrebno uspoređivanje i pretraživanje. Međutim, u ovom prikazu teško je odrediti višekute koji imaju zajednički vrh, a i zajednički bridovi se iscrtavaju dva puta.
30. Kako se vrste elementarnih površine koriste pri modeliranju složenijih površina u računarskoj grafici?*
Površine drugog reda kao što su površina kugle, površina elipsoida ili cilindra mogu poslužiti kao elementarne površine za definiranje modela složenijih površina u trodimenzionalnom prostoru. Ova skupina površina definirana je implicitnom jednadžbom oblika:
f(x,y,z) = ax2 + by2 + cz2 + 2dxy + 2eyz + 2fxz + 2gx + 2hy + 2jz + k = 0
Vrsta površine određena je vrijednostima parametara a, b, c, d, e, f, g, h, i, j i k.
*31. Što predstavlja pojam prikazne transformacije?
*32. Što predstavlja pojam otvora u računarskoj grafici?
33. Opišite tehniku polutonske aproksimacije i njene primjene.
34. Kako se na objektivan način opisuje boja?
35. Što su metameri?
36. Navedite primjere modela boje prema namjenama.
37. Opišite CMY model boje, njegove značajke i primjenu.
38. Na koji se način ostvaruje animacija?
39. Opišite primjenu linearne interpolacije u animaciji.
40. Što predstavlja pojam "slerping" u računarskoj grafici.
Napomena 1: za pitanja 31. - 40. točne odgovore treba potražiti samostalno u tekstu udžbenika.
Napomena 2: pitanja s oznakom * odnose se na dijelove teksta koji nisu obvezatni dio gradiva za predmet "Inženjerska grafika i prezentacija".
Odgovori na postavljena pitanja.
Povratak na: Početak stranice | Sadržaj
Inženjerska grafika, Copyright © D.Begusic