[The link bar feature is not available in this web]  ||| Natrag: Projekcije | Gore: Matematički temelji računarske grafike | Naprijed: Crtanje površina |

Crtanje primitivnih oblika

Prikazivanje slika objekata na rasterskim prikaznim uređajima zahtijeva pretvorbu idealnih slika u rasterski prikaz (scan conversion) s pikselima kao osnovnim elementima prikaza. Izgled, dimenzije i međusobni odnos piksela se razlikuju u pojedinim sustavima. U našim razmatranjima možemo prihvatiti aproksimaciju oblika piksela kao kružića sa središtem na sjecištima horizontalnih i vertikalnih pravaca koji tvore rešetku (koordinate sjecišta su cjelobrojne). Postupak pretvorbe idealne slike u rasterski prikaz podrazumijeva određivanje razine svjetloće i/ili boju piksela u rasteru. Budući da se ova pretvorba obavlja svaki put kad treba prikazati neku sliku (ako nije u cijelosti pohranjena u memoriji), cilj je iznaći i primijeniti takve pretvorbene algoritme koji zahtijevaju minimalan broj procesorskih operacija. Pri tome je važno  korištenje cjelobrojne aritmetike i inkrementalnih metoda kod kojih se pretvorba odvija piksel po piksel (uz korištenje rezultata proračuna za prethodni piksel).

Rasterski prikaz ravnih crta

Algoritmi za rasterski prikaz ravnih crta proračunavaju koordinate piksela na 2D rasteru koji su najbliži idealnoj, beskonačno uskoj ravnoj crti.  Poželjne značajke prikazane ravne crte uključuju:

• jednolik intenzitet crte čitavom dužinom,

• jednolik intenzitet crte neovisno o nagibu,

• mogućnost proizvoljnog odabira širine crte,

• mogućnost proizvoljnog oblikovanja krajeva.

Osnovni je problem crtanje kose ravne crte širine jednog piksela na dvorazinskom rasterskom prikaznom uređaju. Za tu svrhu razvijen je niz algoritama s ciljem pojednostavljenja i ubrzanja postupka.

Osnovni inkrementalni algoritam

Najjednostavniji pristup temelji se na proračunu piksel po piksel na osnovi eksplicitnog oblika jednadžbe pravca.

Algoritam se sastoji od sljedećih koraka:

• proračun nagiba pravca m = Dy/Dx (|m| < 1),

• proračun nove vrijednosti x_i povećanjem prethodne vrijednosti za 1,

• proračun vrijednosti y_i = m x_i + B,

• isticanje piksela (x_i, Round(y_i)) gdje je Round (y_i) = Floor (0.5 + y_i).

Funkcija Round zaokružuje vrijednost realnog broja na najbliži cijeli broj. Ona se može realizirati pomoću funkcije Floor koja pretvara realni broj u cijeli broj odbacivanjem decimalnog dijela. 

Osnovni inkrementalni algoritam odabire točke koje su najmanje udaljene od idealne crte.  Ovaj algoritam nije učinkovit jer se u svakoj iteraciji obavljaju operacije množenja i zbrajanja s realnim ili (racionalnim) brojevima kao i poziv funkcije Floor.

*Digitalni diferencijalni analizator

Nedostatci osnovnog inkrementalnog algoritma mogu se velikim dijelom otkloniti ako se algoritam izmijeni na način da se izbjegne množenje realnih brojeva (koje predstavlja vrlo zahtjevnu operaciju za procesor).

Množenje se može izbjeći ako se izraz za proračun vrijednosti koordinate y napiše na sljedeći način:
        y_i+1 = m x_i+1 + B = m (x_i+Dx) + B = y_i + m Dx
Uz  izbor Dx = 1  slijedi:
        y_i+1 = y_i + m
Ako je |m| > 1 mijenjaju se uloge x i y koordinata u algoritmu:
        Dy = 1
        Dx = Dy/m = 1/m

Na taj način vrijednosti x i y koordinata se povećavaju u malim koracima za vrijednost 1 ili -1 < m < 1. Ovakav algoritam naziva se digitalni diferencijalni analizator (DDA). DDA u osnovi predstavlja algoritam za numeričko rješavanje diferencijalnih jednadžbi istovremenim uvećavanjem koordinata x i y za vrijednosti proporcionalne njihovim prvim derivacijama. Nedostatak ovog algoritma proizlazi iz nepreciznosti prikaza realnih brojeva u digitalnim procesorima. Dodavanje ne sasvim točne vrijednosti unosi kumulativnu pogrešku i otklon od stvarne vrijednosti (za kratke crte razina pogreške je prihvatljiva).

*Algoritmi temeljeni na cjelobrojnoj aritmetici

Računska složenost DDA algoritma, iako je značajno smanjena u odnosu na osnovni inkrementalni algoritam, još uvijek nije optimalna jer sadrži operacije s realnim brojevima. Daljnji napredak na ovom području ostvaren je razvitkom algoritama koji su temeljeni na cjelobrojnoj aritmetici. Značajnu ulogu u tom razvitku ima Bresenhamov algoritam utemeljen na inkrementalnoj tehnici. Ta tehnika daje najbolju aproksimaciju idealnih crta u smislu minimizacije pogrješke (odnosno udaljenosti odabranih točaka od idealnih crta), a može se primjeniti i na crtanje kružnica. Poboljšane inačice ovog algoritma temelje se na primjeni tehnike središnje točke (Pitteway, Van Aken). Međutim za slučaj crtanja ravnih crta i ove formulacija svode se na Bresenhamovu formulaciju.

U formulaciji algoritma središnje točke pretpostavlja se da je nagib pravca između 0 i 1. Za pravce s nagibima izvan ovog intervala primjenjuje se tehnika zrcaljenja oko koordinatnih osi. Pravac se preslikava u odgovarajući pravac s nagibom unutar navedenog intervala čime se omogućava primjena algoritma središnje točke. Na kraju se aproksimacija dijela pravca  definirana primjenom algoritma zrcali u obrnutom smjeru.

Označimo donju lijevu točku koordinatama (x₀,y₀), a gornju desnu točku koordinatama (x₁,y₁). Pretpostavimo da je posljednja odabrana točka P s koordinatama (x_p,y_p) te da je potrebno odabrati sljedeću desnu točku. Odabir se svodi na izbor između dviju mogućih točaka: susjedne točke D do koje se dolazi pomakom udesno za jedan i točke GD do koje se dolazi pomakom za jedan udesno i za jedan prema gore. Potrebno je odrediti koja od te dvije točke je bliža idealnom pravcu. Označimo s T točku sjecišta idealnog pravca s dužinom koja povezuje točke D i GD. Izbor sljedeće točke svodi se na određivanje kojoj je od te dvije točke bliža točka T. U Bresenhamovoj formulaciji algoritma izračunava se razlika udaljenosti točke T do točke D i do točke GD te se na temelju predznaka rezultata određuje koja je od tih dviju točaka bliža idealnom pravcu.

*Algoritam središnje točke

U formulaciji temeljenoj na središnjoj točci taj se postupak odvija na drugačiji način. Prvo se definira središnja točka S(x_p+1, y_p+1/2) kao točka polovišta dužine koja povezuje točke D i GD. Odluka se donosi na temelju informacije o položaju središnje točke u odnosu na idealni pravac. Ako je središnja točka S ispod idealnog pravca onda je očito točka GD bliža idealnom pravcu. Ako je središnja točka S iznad središnje točke onda je točka D bliža idealnom pravcu.

Da bi se ovaj postupak odvijao na učinkovit način definira se varijabla odluke d koja se rekurzivno izračunava od koraka do koraka. Na temelju predznaka varijable odluke određuje se sljedeća točka. U svakom koraku algoritam vrši izbor između dvije točke na temelju predznaka varijable odluke te uvećava varijablu odluke za jednu od dvije moguće vrijednosti u ovisnosti o izabranoj točki.

U nastavku je formuliran algoritam za crtanje ravne crte temeljen na tehnici središnje točke.

Nagib idealnog pravca koji povezuje točke (x₀,y₀) i (x₁,y₁), uz uvjet: 0<m<1 ( za druge vrijednosti m primjenjuje se zrcaljenje oko glavnih osi), može se odrediti na sljedeći način:
        m = dy/dx
gdje je dy = y₁ - y₀  i  dx = x₁ - x_0.
Eksplicitni oblik jednadžbe pravca tada se može napisati u sljedećem obliku:
        y = (dy/dx) x + B
a implicitni oblik jednadžbe pravca u sljedećem obliku:
        F(x,y) = ax + by + c = 0
gdje je a = dy,    b = -dx,   c = B dx.
Na temelju svojstava implicitnog oblika jednadžbe pravca poznato je da vrijede sljedeći odnosi između točke i pravca:
        F(x,y) = 0  => točka  je na pravcu
        F(x,y) < 0  => točka je ispod pravca
        F(x,y) > 0  => točka je iznad pravca
Očito je da vrijednost F(x,y) gdje su x i y koordinate središnje točke S(x_p+1, y_p+1/2) možemo koristiti kao varijablu odluke.
Varijabla odluke definirana je na sljedeći način:
        d = F(S) = F(x_p+1, y_p+1/2) = a(x_p+1) + b(y_p+1/2) + c
U ovisnosti o predznaku varijable odluke algoritam se  na sljedeći način:
1.a. Ako je d > 0  => izbor točke GD;
2.a. Nova vrijednost varijable odluke bit će u tom slučaju d_n =  d + D_D ;
(Objašnjenje: varijabla odluke je d_n = F(x_p+2, y_p+1/2) = a(x_p+2) + b(y_p+1/2) + c, a promjena varijable odluke  D_D = d_n - d = a = dy)
        1.b. Ako je d < 0  => izbor točke D ;
        2.b. Nova vrijednost varijable odluke bit će u tom slučaju d_n =  d + D_GD ;
(Objašnjenje: varijabla odluke je d_n = F(x_p+2, y_p+3/2) = a(x_p+2) + b(y_p+3/2) + c,  a promjena varijable odluke D_GD = d_n - d = a + b = dy - dx).
Ako je d = 0 izbor između dvije točke je proizvoljan jer su obje jednako udaljene od idealnog pravca.

Ako se zna da je prva točka lijeva početna točka (x₀,y₀), a prva središnja točka (x₀+1, y₀+1/2) tada se može odrediti prva vrijednost varijable odluke: d = a + b/2. Zbog razlomka b/2 prikladno je umjesto F(S) koristiti 2F(S) u formulaciji algoritma. Time se osigurava da algoritam koristi isključivo cijele brojeve.

Ispunjavanje primitivnih oblika

Mogućnost ispunjavanja primitivnih oblika kao što su pravokutnici, kružnice, elipse i mnogokuti značajno doprinosi vrijednosti i primjenjivosti grafičkog sustava. Pri tome je moguće ispunjavanje bojom ili određenim uzorkom. Osnovni koraci u tom postupku su:

• izbor piksela koje treba ispuniti (ovisi o obliku),

• izbor vrijednosti koju treba pridijeliti odabranim pikselima (ovisi o načinu ispunjavanja: bojom ili uzorkom).

Izbor piksela koje treba ispuniti odvija se u sljedećim koracima:

• skaniranje po horizontalnim crtama (retcima piksela),

• proračun presjecišta horizontalne crte i primitivnog oblika inkrementalnim algoritmom (odabiru se točke koje leže unutar oblika),

• poredavanje presjecišta po veličini x koordinate,

• ispunjavanje odsječaka koji leže unutar primitivnog oblika (između neparnih i parnih presjecišta).

U slučaju ispunjavanja primitivnog oblika bojom odabranim pikselima pridjeljuje se prethodno odabrana konstantna vrijednost. Način ispunjavanja mnogokutnog oblika bojom ilustriran je na slici 3.10. U slučaju ispunjavanja primitivnog oblika uzorkom algoritam se upotpunjuje dijelom koji upravlja izborom vrijednosti pojedinog piksela. Vrijednosti pojedinih piksela preuzimaju se određenim redoslijedom iz dijela memorije u kojem je definiran uzorak.

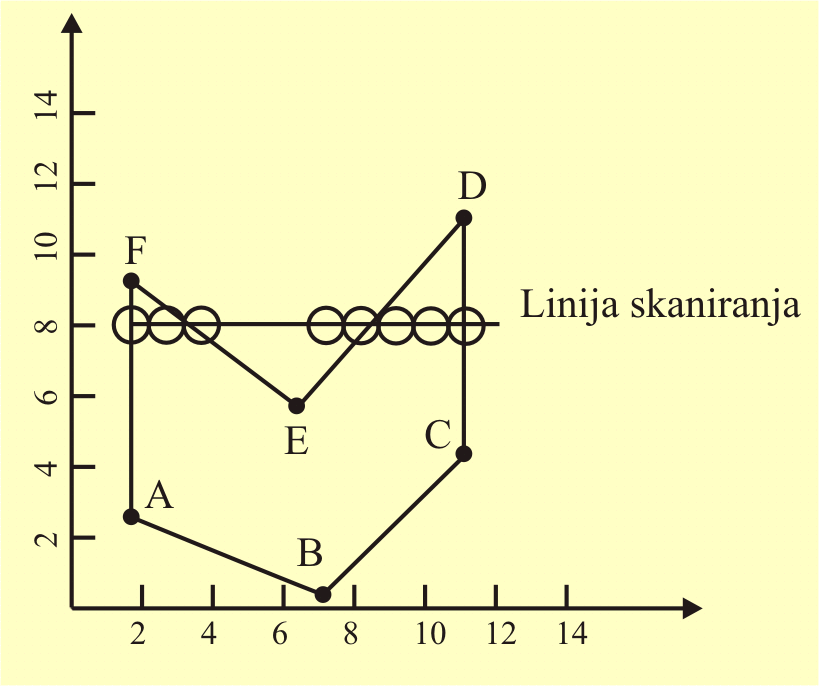
Slika 3.10  Primjer ispunjavanja mnogokutnog oblika bojom.

Crtanje krivulja

Mnogi objekti iz stvarnog svijeta, ali i iz virtualnih svjetova, koje se prikazuje primjenom računarske grafike omeđeni su glatkim krivuljama ili plohama. Najčešći je slučaj da egzaktan matematički model takvog objekta ne postoji ili je presložen za primjenu u stvarnom vremenu. Stoga je nužno kreirati približan matematički model koji omogućava grafičko predstavljanje objekta na zadovoljavajući način.

Najjednostavniji pristup modeliranju krivulje je linearna aproksimacija (prvog reda) po dijelovima (Slika 3.11). Krivulja se aproksimira višestrukim crtama (niz povezanih ravnih crta) ili mnogokutima. Točnost aproksimacije određena je brojem linearnih segmenata kojima se aproksimira pojedini dio krivulje. Za visoku razinu podudarnosti linearnog aproksimacijskog modela i željene krivulje potreban je velik broj linearnih segmenata.

Slika 3.11 Primjer modeliranja krivulje linearnim segmentima.

Veća razina podudarnosti odnosno bolja aproksimacija uz manji broj pojedinačnih segmenata može se ostvariti primjenom aproksimacija višeg reda. Na taj način smanjuje se potrebna količina memorije i olakšava interaktivni rad pri modeliranju. Najčešće se koriste aproksimacije trećeg reda jer aproksimacije nižeg reda ne daju dovoljno fleksibilnosti za oblikovanje različitih krivulje, a aproksimacije višeg reda su računski zahtjevnije i složenije za primjenu.

Postoji više oblika matematičkog prikaza krivulja za aproksimacije višeg reda: eksplicitni, implicitni i parametarski.

Parametarske krivulje trećeg reda

Parametarske krivulje trećeg reda najčešće se koriste za modeliranje krivulja u računarskoj grafici jer omogućavaju dovoljno fleksibilnosti za oblikovanje različitih krivulje uz prihvatljivu razinu složenosti. Model krivulje se specificira po odsječcima polinomima trećeg reda. Svaki odsječak Q opisan je s tri funkcije (polinoma trećeg reda) x, y i z parametra t na sljedeći način: Q(t) = [x(t) y(t) z(t)] gdje je

        x(t) = a_x t³ + b_x t² + c_x t + d_x
        y(t) = a_y t³ + b_y t² + c_y t + d_y
        z(t) = a_z t³ + b_z t² + c_z t + d_z
        uz 0 ≤ t ≤ 1.

Ako definiramo vektor potencija parametra t na sljedeći način:

        T = [ t³  t²  t  1]

te matricu koeficijenata triju polinoma na sljedeći način:

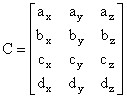
tada možemo pisati izraz za model odsječka krivulje u sažetom obliku

        Q(t) = T C.

Definicija odsječka krivulje Q(t)

Polinom trećeg stupnja kao model odsječka krivulje ima 4 nepoznata koeficijenta što zahtijeva 4 uvjeta za njihovo određivanje. Na taj način dobija se sustav od ukupno 4 jednadžbe s 4 nepoznanice. Uvjeti mogu biti: krajnje točke, vektor smjera tangente ili kontinuitet u točkama dodira pojedinih odsječaka.

Hermiteove krivulje i Bezierove krivulje zadovoljavaju kriterije G¹ i C¹ kontinuiteta uz određene uvjete, dok B-krivulje i b-krivulje zadovoljavaju kriterije C¹ i C² kontinuiteta.

Matrica koeficijenata C može se izraziti kao umnožak bazne matrice M i geometrijskog vektora G koji sadrži zadane geometrijske uvjete (npr. koordinate točaka):

        C = M G

Izraz za parametarski model odsječka krivulje tada možemo napisati na sljedeći način:

        Q(t) = T M G

Promatramo li samo jednu komponentu vektora Q(t) npr. x(t) dobivamo sljedeći izraz:

        x(t) = T M G_x

Označimo li umnožak vektora T i matrice M s B (B=TM) možemo pisati :

        Q(t) = B G

Elementi matrice B su polinomi trećeg reda parametra t. Na taj način vidimo da je krivulja predstavljena kao težinski zbroj elemenata geometrijskog vektora, gdje su težinski faktori polinomi parametra t.

Za svaku pojedinu vrstu krivulja definirana je bazna matrica M i geometrijski vektor G.

Bezierove krivulje

Bezierove krivulje definirane su sljedećim geometrijskim uvjetima:

• dvije krajnje točke P₁  i P₄.

• dvije kontrolne točke P₂ i P₃ koje određuju vektore smjera u krajnjim točkama R₁ i  R₄. 

Pomoću dviju kontrolnih točaka posredno su definirani vektori smjera tangenti R₁ i R₄ u dvjema krajnjim točkama. Vektor smjera tangente u početnoj točci odgovara derivaciji krivulje Q(t) za vrijednost parametra t=0, dok  vektor smjera tangente u krajnjoj točci odgovara derivaciji krivulje Q(t) za vrijednost parametra t=1:

        R₁ = Q’(0) = 3(P₂-P₁)

        R₄ = Q’(1) = 3(P₄-P₃)

Elementi geometrijskog vektora su četiri zadane točke. Geometrijski vektor za Bezierove krivulje definiran je na sljedeći način:

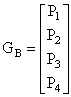
Bazna matrica za Bezierove krivulje definirana je na sljedeći način:
       

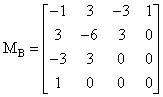
Imajući u vidu da je odsječak krivulje opisan izrazom:

        Q(t) = T M_B G_B

uvrštenjem bazne matrice i geometrijskog vektora dobivamo sljedeći oblik jednadžbe odsječka Bezierove krivulje:

        Q(t) = (1-t)³ P₁ + 3t (1-t)² P₂ + 3t² (1-t) P₃ + t³ P₄

Polinomi koji predstavljaju koeficijente pojedinih točaka u ovom izrazu nazivaju se Bernsteinovi polinomi. Na slici 3.13 a) prikazan je primjer crtanja odsječka Bezierove krivulje, a na slici 3.13 b) primjer dvaju spojenih odsječaka Bezierovih krivulja.

a)

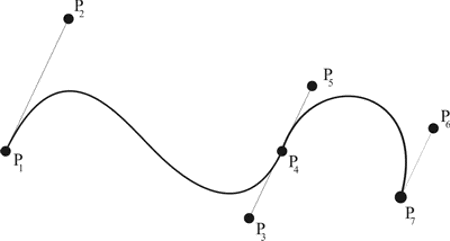
b)

Slika 3.13 a) Primjer crtanja odsječka Bezierove krivulje,  b) Primjer dvaju spojenih odsječaka Bezierovih krivulja.

Uvjet za G¹ kontinuitet jest da točke P₃, P₄ i P₅ moraju biti različite i kolinearne

        P₃ - P₄ = k (P₄ - P₅),   k > 0

Uvjet  za C¹ kontinuitet jest da je k = 1.

*Pretvorba oblika krivulja

Sve skupine krivulja predstavljene matričnim umnoškom Q(t)=TMG moguće je međusobno pretvarati iz jednih u druge npr. krivulje predstavljenu baznom matricom M₁ i geometrijskim vektorom G₁ moguće je predstaviti drugom baznom maticom M₂ i odgovarajućim geometrijskim vektorom G₂.  Važno je da mora biti ispunjen uvjet:

        M₂ G₂= M₁ G₁

Nepoznati geometrijski vektor G₂ može se izračunati na sljedeći način:

        G₂ =  M₂^-1M₁ G₁

Na taj način može se npr. krivulja predstavljena baznom matricom i geometrijskim vektorom za Hermiteove krivulje transformirati u prikaz baznom matricom i geometrijskim vektorom za Bezierove krivulje. Različite vrste krivulja imaju različite prednosti za pojedine vrste primjena. Prednosti različitih vrsta krivulja mogu se najbolje iskoristiti u kombiniranom načinu prikaza krivulja. Često se krivulja se predstavlja korisniku putem sučelja kao Bezierova ili Hermiteova, dok je unutrašnja reprezentacija B-krivulja. Npr. u PostScript-u se krivulje predstavljaju korisniku kao Hermiteove dok im je unutrašnja predstava Bezierova.

Bezierove i Hermiteove krivulje posebice su prikladne za interaktivnu manipulaciju zbog razumljivosti djelovanja korisnika putem kontrolnih točaka i vektora tangenti. B-krivulje prikladne su za unutarnje predstavljanje krivulja zbog svoje općenitosti.

*Načini crtanja parametarskih krivulja

Postupak crtanja parametarskih krivulja uključuje određivanje diskretnog skupa točaka na modelu krivulje i iscrtavanje ravnih crta koje ih povezuju. Pri tome su mogući različiti pristupi uključujući:

• iterativni proračun x(t), y(t) i z (t) za niz bliskih rastućih vrijednosti parametra t,

• rekurzivna podjela do zadovoljavajuće bliskosti kontrolnih točaka samoj krivulji,

• hibridni pristup kao kombinacija iterativnog i rekurzivnog načina.

Iterativni proračun odvija se na način da se vrijednosti koordinanata x(t), y(t), i z(t) pojedinih točaka izračunavaju za niz vrijednosti parametra t međusobno udaljenih za unaprijed određeni konstantan iznos d. Proračunate točke spajaju se ravnim crtama. Problem ovakvog pristupa je u tome što se unaprijed treba odrediti razmak točaka s obzirom na parametar t. Prevelik razmak rezultira slabom kvalitetom aproksimacije dok premalen razmak rezultira nepotrebnim proračunskim opterećenjem. Izravnom primjenom ovog pristupa za Bezierove krivulje potrebno je 9 množenja i 10 zbrajanja po točci. Međutim algoritam se može numerički optimizirati te svesti na svega 9 zbrajanja po točci.

Rekurzivna podjela odvija se na način da se između dvije izračunate točke umeće treća točka. Rekurzivna podjela zaustavlja se adaptivno kada odsječak krivulje postane dovoljno ravan da se može aproksimirati ravnom crtom. Pojedinosti postupka različite su za pojedine vrste krivulja. Ovaj pristup je posebice prikladan za Bezierove krivulje. Na taj način postiže se računska složenost od 6 zbrajanja i 6 posmaka. Kriterij ravnoće je da udaljenosti unutarnjih kontrolnih točaka do spojnice krajnjih točaka moraju biti manje od zadane vrijednosti (slika 3.14). Prednost ovog pristupa je u tome što se izbjegavaju nepotrebni proračuni, a nedostatak je što se mora ispitivati ravnoća pojedinih dijelova.

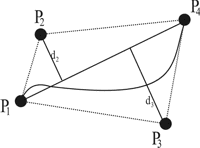
Slika 3.14  Primjer primjene kriterija ravnoće pri rekurzivnom pristupu crtanju Bezierovih krivulja.

Hibridni pristup kombinira najbolja svojstva iterativnog i rekurzivnog pristupa. U osnovi se može opisati kao iterativni proračun s adaptivnim korakom.  

*Glatkoća krivulje na spoju odsječaka

Geometrijski kontinuitet definiran je na sljedeći način:

• geometrijski kontinuitet G⁰  -  neprekinutost krivulje u točki dodira odsječaka,

• geometrijski kontinuitet G¹  -  jednakost vektora smjera tangente u točki dodira odsječaka.

Izraz za vektor smjera tangente može se izračunati deriviranjem izraza za Q(t)

        .

Parametarski kontinuitet definiran je na sljedeći način:

• parametarski kontinuitet C¹  -  jednakost parametara t u točki dodira odsječaka,

• parametarski kontinuitet Cⁿ  -  jednakost n-te derivacije Q(t) u točki dodira odsječaka.

Odnos parametarskog i geometrijskog kontinuiteta može se sažeti na sljedeći način:
        C¹ => G¹
tj. parametarski kontinuitet implicira geometrijski kontinuitet, dok obrat općenito ne vrijedi.

Na slici 3.12 ilustrirani su primjeri krivulja različitih razina glatkoće izraženih u smislu parametarskog kontinuiteta.

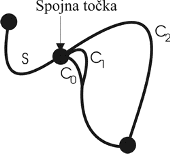
Slika 3.12  Ilustracija parametarskog kontinuiteta C⁰ , C¹ i C².

Povratak na: Početak stranice | Sadržaj

[The link bar feature is not available in this web]  ||| Natrag: Projekcije | Gore: Matematički temelji računarske grafike | Naprijed: Crtanje površina |

Inženjerska grafika, Copyright © D.Begusic