[The link bar feature is not available in this web] ||| Natrag: Transformacije grafičkih objekata | Gore: Matematički temelji računarske grafike | Naprijed: Crtanje primitivnih oblika |
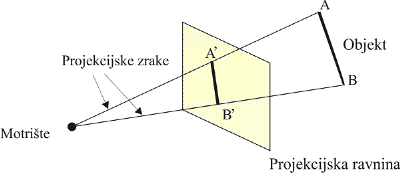
U računarskoj grafici često je potrebno objekte iz prostora višeg reda prikazati u prostoru nižeg reda. Primjer takvog slučaja je prikaz scene definirane u 3D prostoru na dvodimenzionalnom prikaznom uređaju kao što je zaslon računala. Postupak preslikavanja objekta iz prostora višeg reda u prostor nižeg reda naziva se projekcija. U okviru ovog razmatranja mi ćemo se ograničiti na područje ravninskih geometrijskih projekcija. Pored njih postoje i neravninske i negeometrijske projekcije kod kojih se projicira na neku zakrivljenu površinu odnosno uz uporabu zakrivljenih projekcijskih zraka (takve su npr. mnoge kartografske projekcije). Ravninske geometrijske projekcije se u načelu odvijaju na način da projekcijske zrake koje izlaze iz projekcijskog središta prolaze kroz sve točke objekta i presjecaju projekcijsku ravninu tvoreći u njoj oblik projekcije. Postoji više vrsta ravninskih geometrijskih projekcija koje su prikladne za različite namjene, a osnovne dvije skupine su perspektivne projekcije i paralelne projekcije. Temeljna razlika je u odnosu projekcijskog središta i projekcijske ravnine. Kod paralelnih projekcija udaljenost projekcijskog središta i projekcijske ravnine je beskonačna, dok je kod perspektivnih projekcija ta udaljenost konačna.

a)
b)
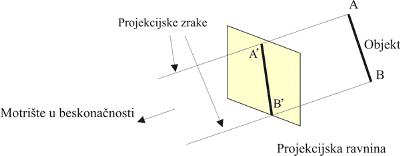
Slika 3.6 Primjer projekcije dužine: a) paralelna projekcija, b) perspektivna projekcija.
Ortogonalna projekcija preslikava sve točke objekta paralelnim zrakama na određenu ravninu. Slučaj ortogonalne projekcije na koordinatne ravnine posebno je jednostavan.
Ortogonalna projekcija na xy-ravninu odgovara odabiru konstantne vrijednosti z koordinate iznosa 0 tj. z=0. Matematički se ova operacija može definirati kao množenje vektora s dijagonalnom matricom čiji su svi elementi jednaki jedinici osim trećeg koji je jednak nuli.
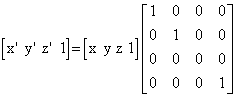
Na sličan način ortogonalna projekcija na xz-ravninu odgovara odabiru konstantne vrijednosti y koordinate iznosa 0 tj. y=0. Matematički se ova operacija može definirati kao množenje vektora s dijagonalnom matricom čiji su svi elementi jednaki jedinici osim drugog koji je jednak nuli.
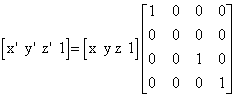
Ortogonalna projekcija na yz-ravninu odgovara odabiru konstantne vrijednosti x koordinate iznosa 0 tj. x=0. Matematički se ova operacija može definirati kao množenje vektora s dijagonalnom matricom čiji su svi elementi jednaki jedinici osim prvog koji je jednak nuli.
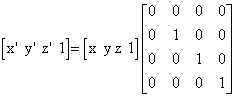
Kosa projekcija ima sličnost s ortogonalnom u tome što su projekcijske zrake međusobno paralelne. Razlika je tome što nisu ortogonalne na projekcijsku ravninu nego na nju upadaju pod nekim kutom.
Slike dobivene ortogonalnom projekcijom određene su paralelnošću projekcijskih zraka. U praksi je često zanimljiva vrsta projekcije kod koje projekcijske zrake nisu paralelne. Takav je slučaj kod fotografije i kod ljudskog vida. Fotografija predstavlja projekciju scene iz 3D prostora na dvodimenzionalnu ravninu. Projekcijske zrake u tom slučaju izviru iz jedne točke na konačnoj udaljenosti od projekcijske ravnine. Takva projekcija naziva se perspektivna ili fotografska.
Primjer perspektivne projekcije ilustrirana je slikom 3.7. Promatrač se nalazi na udaljenosti h od projekcijske ravnine. Bridovi xa i xb preslikavaju se u dužine x'a i x'b.
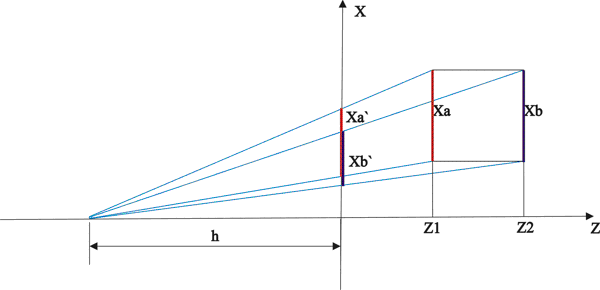
Slika 3.7 Ilustracija postupka perspektivne projekcije.
Zbog sličnosti trokuta može se pisati
![]()
odnosno
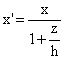
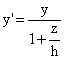
Na temelju ovih dvaju izraza može se definirati transformacijska matrica perspektivne projekcije te se postupak svodi na množenje vektora pojedine točke s tom matricom.
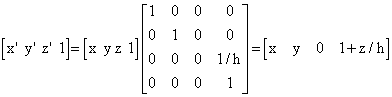
Povratak na: Početak stranice | Sadržaj
[The link bar feature is not available in this web] ||| Natrag: Transformacije grafičkih objekata | Gore: Matematički temelji računarske grafike | Naprijed: Crtanje primitivnih oblika |
Inženjerska grafika, Copyright © D.Begusic