[The link bar feature is not available in this web] ||| Natrag: Transformacija koordinata | Gore: Stvaranje slikovnog prikaza | Naprijed: Napredne tehnike grafičkog izražavanja |
Općenito se na zaslonu prikazuje dio cjelovitog prostora odnosno skupa objekata. Dio prostora odnosno skupa objekata koji nije dio prikazane slike treba isključiti iz prikaza odnosno iz prikazne datoteke. Osnovni postupci su izrezivanje ("scissoring") pri kojem crte izvan područja zaslona postaju nevidljive i odrezivanje ("clipping") pri kojem se dio slike izvan područja zaslona potpuno odbacuje tako što se stvara nova prikazna datoteka.
Postupak odrezivanja pojedinačnih točaka temelji se na provjeri uvjeta određenih sljedećim nejednadžbama:
xmin < x < xmax
ymin <
y < ymax
Za odrezivanje crte dovoljno je uzeti u obzir krajnje točke. Crta čije su obje krajnje točke unutar odreznog pravokutnika je trivijalno prihvatljiva. Ukoliko obje krajnje točke ne leže unutar odreznog pravokutnika treba utvrditi da li postoji i gdje se nalazi presjecište crte i bridova odreznog pravokutnika te na temelju toga odrediti da li postoji i koji je dio crte prihvatljiv. Izravan pristup zahtijevao bi rješavanje dviju jednadžbi s operacijama množenja i dijeljenja za svaki rub odreznog pravokutnika. Učinkovitiji pristup problemu odrezivanja crte je primjena prikladnog optimiziranog algoritma. Primjer takvog algoritma je Cohen-Sutherland algoritam kojim se izbjegava proračun presjecišta u slučajevima kada se jednostavnijim testovima može utvrditi trivijalna prihvatljivost ili neprihvatljivost crte.
|
Osnovni koraci algoritma su:
|
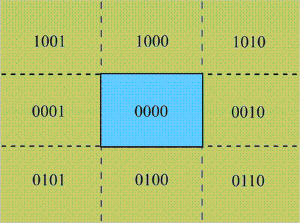
Ravnina odreznog pravokutnika dijeli se na 9 područja određenih pravcima bridova odreznog pravokutnika. Svakom području pridružuje se 4-bitni kod određen položajem područja u odnosu na pravce bridova odreznog pravokutnika. Način definiranja kodova prikazan je u tablici 4.1., a način njihovog raspoređivanja na slici 4.2.
|
bit |
položaj |
uvjet |
|
1 |
iznad pravca gornjeg ruba |
y > ymax |
|
2 |
ispod pravca donjeg ruba |
y < ymin |
|
3 |
desno od pravca desnog ruba |
x > xmax |
|
4 |
lijevo od pravca lijevog ruba |
x < xmin |
Tablica 4.1 Način definiranja kodova u Cohen-Sutherland algoritmu.
Ako je navedni uvjet ispunjen odgovarajućem bitu pridružuje se vrijednost 1, a u suprotnom vrijednost 0. Npr. kod 1010 znači da se točka nalazi: iznad pravca gornjeg ruba i desno od pravca desnog ruba.

Slika 4.2 Raspored kodova po područjima u Cohen-Sutherland algoritmu.
|
Algoritam se može sažeti i na sljedeći način:
|
Kooordinate presjecišta se izračunavaju uvrštavanjem poznate koordinate ruba odreznog pravokutnika u jednadžbu pravca na kojem leži crta. Na slici 4.3 prikazani su neki karakteristični slučajevi položaja crta u odnosu na površinu prikaznog uređaja.
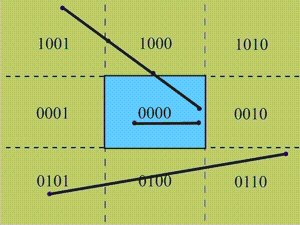
Slika 4.3 Primjeri položaja crta u odnosu na površinu prikaznog uređaja.
2D algoritam za odrezivanje primjenjuje se nakon projekcije iz 3D svijeta. Moguća je prilagodba algoritma primjeni prije projekcije tako da se unaprijed izdvoji dio scene koji će se vidjeti na zaslonu nakon projekcije. Takav algoritam se temelji na definiciji ispitne piramide. Položaj ispitne piramide u odnosu na motrište i promatrane objekte prikazan je na slici 4.4.
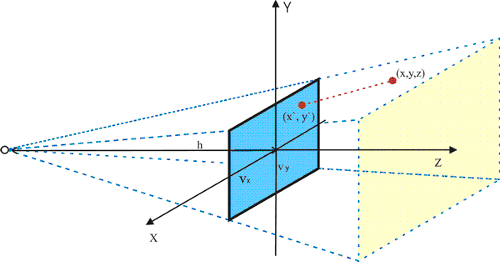
Slika 4.4 Položaj ispitne piramide u odnosu na motrišta, ravninu zalona i promatrani objekt.
Točke unutar ispitne piramide moraju zadovoljavati izraze:
x’ = x h/(z+h) < vx
y’ = y h/(z+h) < vy
gdje su:
x’,y’ -
koordinate u ravnini zaslona
h -
udaljenost zaslona od promatrača
2vx,
2vy - dimenzije zaslona
Gornje nejednadžbe mogu se napisati u obliku:
-(z+h) <
x h/vx
<
(z+h)
-(z+h) <
y h/vy
<
(z+h)
Na
temelju tih nejednadžbi mogu se napisati uvjeti za x i y koordinate koje moraju
zadovoljavati ako se točka nalazi unutar ispitne piramide:
- vx(1+z/h) <
x <
vx(1+z/h)
- vy(1+z/h) < y < vy(1+z/h)
Povratak na: Početak stranice | Sadržaj
[The link bar feature is not available in this web] ||| Natrag: Transformacija koordinata | Gore: Stvaranje slikovnog prikaza | Naprijed: Napredne tehnike grafičkog izražavanja |
Inženjerska grafika, Copyright © D.Begusic