||| Natrag: Boja u računarskoj grafici | Gore: Napredne tehnike grafičkog izražavanja | Naprijed:  |

 

ANIMACIJA

Pojam animacija podrazumijeva sve promjene koje imaju vidljivi učinak, a to uključuje vremensku promjenu: položaja (kretanje), oblika, boje, transparentnosti, strukture, osvjetljenja, položaja gledišta, žarišta i drugo.

Animacija se primjenjuje u edukaciji, industriji zabave, industrijskim upravljačkim sustavima, znanstvenoistraživačkoj djelatnosti i drugim područjima.

Poseban naziv - znanstvena predodžba (scientific visualization) označava primjenu računarske grafike uključujući animaciju, obradbu signala, računarsku geometriju i teoriju baza podataka za znanstvenoistraživačke namjene. Složeni simulacijski postupci, proračuni i mjerenja mogu rezultirati velikim količinama podataka čija preglednost se značajno može poboljšati primjenom računarske grafike.

Osnovni postupci u animaciji uključuju sljedeće korake:

  • na temelju zamisli i skice kreira se niz ključnih slika (key frames) u kojima su animirani entiteti u ekstremnim ili karakterističnim položajima,

  • na temelju ključnih slika stvara se niz međuslika i tako upotpunjuje niz (ovaj postupak prikladan je za primjenu računala),

  • prije primjene računala nužna je digitalizacija slike (optičkim skaniranjem, digitalizatorskom pločom ili crtanjem pomoću računala),

Primjena računala posebno je prikladna za automatizaciju postupaka generiranje međuslika i bojanje slika. Pored toga moguća je primjena tehnike "pan-zoom " za testiranje animacije. Slika smanjene rezolucije pohranjuje se u okvirni međuspremnik, zatim se pomiče u središte zaslona (ovaj postupak na engleskom se zove panning) i povećava tako da zauzme čitavu površinu zaslona (ovaj postupak na engleskom naziva se zooming). Ponavljanjem ovog postupka za niz slika dobija se utisak kontinuiteta. 

Interpolacija

 

Postupak stvaranja međuslika pomoću računala provodi se primjenom tehnika interpolacije. Najjednostavniji pristup stvaranju međuslika temelji se na primjeni linearne interpolacije (ovaj postupak na engleskom se ponekad naziva lerping - linear interpolation). Na temelju poznatih vrijednosti nekog atributa u krajnjim točkama vp i vk (položaj, boja, veličina) vrijednost atributa vm u nizu međuslika može se izračunati na sljedeći način:

        vm = (1-t) vp + t vk         0 <  t < 1

Linearna interpolacija je jednostavna, ali ima niz ograničenja npr. iako generira kontinuirano kretanje ne generira kontinuirane derivacije. Animacija kretanja na takav način izgleda neprirodno. Na slici 5.13. prikazane su ključne slike i međuslike za animaciju dijela putanje lopte. Neprirodnost animacije temeljene na linearnoj interpolaciji posebice se očituje u najvišoj točci putanje gdje dolazi do promjene smjera kretanja.

 

a)                                            b)

Slika 5.13  Linearna interpolacija kretanja lopte: a) ključne slike, b) interpolirane međuslike.

Ograničenja linearne interpolacije mogu se izbjeći primjenom nelinearne interpolacije temeljene na nekoj krivulji f(t) s konstantnom derivacijom u sredini i nultom derivacijom na krajevima. Primjena takve krivulje osigurava kontinuitet derivacije u krajnjim točkama putanje i znatno prirodniji izgled animiranog kretanja. Vrijednost parametra u međuslici tada se izračunava u skledu sa sljedećim izrazom:

        vm = (1-f(t)) vp + f(t) vk    0 <  t < 1

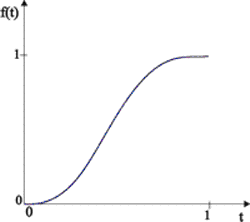
Slika 5.14 Oblik krivulje prikladan za nelinearnu interpolaciju.  

Poseban problem pojavljuje se pri animaciji orijentacije trodimenzionalnog tijela. Ako se orijentacija specificira kutovima zakreta oko tri glavne osi, poznatim kao Eulerovi kutovi, važan je redoslijed specifikacije pojedinih kutova, odnosno redoslijed zakretanja oko pojedinih osi. Zamjenom redoslijeda zakretanja oko pojedinih osi dobiju se različite orijentacije tijela u prostoru. Zbog toga interpolacija Eulerovih kutova rezultira neprirodnim interpolacijama orijentacija u prostoru. Rješenje ovog problema je u primjeni algebarske strukture kvaterniona umjesto Eulerovih kutova.

Kvaternioni su simboli oblika:

        a + bi + cj + dk,

gdje su a, b, c i d realni brojevi koji zadovoljavaju uvjet: a2+ b2+ c2+ d2 = 1.

Može ih se smatrati točkama na jedničnoj sferi u četverodimenzionalnom prostoru. Kvaternioni se množe primjenom zakona distribucije i sljedećih pravila:  i2 = j2 = k2  = -1, ij = k = -ji, jk = i = -kj, ki = j = -ik.

Rotacija za kut j oko jediničnog vektora [b c d]T odgovara kvaternionu  cos j/2 + b sin j/2 i + c sin j/2 j + d sin j/2 k. Provođenje niza uzastopnih rotacija odgovara množenju kvaterniona.

Interpolacija između dva kvaterniona odvija se najkarćom putanjom po sferi i predstavlja prirodno poopćenje postupka linearne interpolacije. Stoga se i naziva sferičnom linearnom interpolacijom (skraćeni engleski naziv je slerp).

Animacijski jezici

Područje razvoja jezika za opis animacija vrlo je dinamično. Razvijen je veći broj animacijskih jezika koji se općenito mogu svrstati u tri skupine:

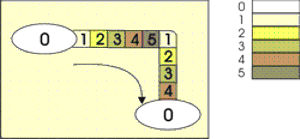
Zapisi u obliku linearnih lista svaki događaj u animaciji opisuju rednim brojem početne i krajnje slike te djelovanjem npr.

        42, 53, B  ROTATE “SLIKA1”, 1, 30

znači: između slika 42 i 53 zakrenuti objekt SLIKA1 oko osi 1 za 30 stupnjeva, pri čemu se zakret za svaku pojedinu sliku određuje iz tablice B.

Jezici opće namjene s ugrađenim animacijskim naredbama pružaju velike mogućnosti, ali zahtijeva značajnu razinu programerske stručnosti. Važna je prednost što se vrijednosti varijabli u jeziku koriste se kao parametri za rutine koje generiraju animaciju. Posebno je zanimljiva mogućnost uporabe jezika više razine za generiranje simulacije pri čemu se generira i animacija kao usporedni proces.

Grafički animacijski jezici temelje se na vizualnom pristupu i izravnom stvaranju animacije umjesto pisanja niza naredaba. Prednost u odnosu na tekstualne jezike je to što animator može izravno promatrati učinak napisanih naredaba.

 

 

Povratak na: Početak stranice | Sadržaj

  ||| Natrag: Boja u računarskoj grafici | Gore: Napredne tehnike grafičkog izražavanja | Naprijed:  |

Inženjerska grafika, Copyright © D.Begusic