![]()
![]()
![]() ||| Natrag: Uvod:
Matematički pristup računarskoj grafici
| Gore: Matematički
temelji računarske grafike
|
Naprijed: Projekcije
|
||| Natrag: Uvod:
Matematički pristup računarskoj grafici
| Gore: Matematički
temelji računarske grafike
|
Naprijed: Projekcije
|
Transformacije grafičkih objekata mogu se prikazati u matričnom obliku na sažet i jednostavan način. Objekti uobičajeno sadrže velik broj točaka pa i transformacije sadrže velik broj istovrsnih aritmetičkih operacija.
|
Ako je općenita transformacija homogene točke u 3D prostoru definirana matricom M tada se njena transformacija može opisati na sljedeći način:
|
Transformacija objekta obavlja se tako da se ista transformacija primijeni na sve njegove točke.
Transformacijom translacije obavlja se pomak točke V u točku V’ za iznos (Tx,
Ty). Koordinate transformirane točke mogu se odrediti sljedećim
dvjema jednadžbama:
x’ = x +
Tx
y’ = y +
Ty
Sažetiji način zapisa ovog proračuna u homogenom prostoru može se izvesti ako definiramo matricu translacije T na sljedeći način:
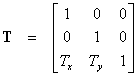
U homogenom prostoru možemo odabrati vrijednost dodatne koordinate npr. iznosa 1 pa matrična jednadžba za proračun koordinata transformirane točke ima sljedeći oblik:
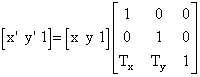
Ovakva jednadžba može se napisati u sažetom obliku na sljedeći način:
V’ = V T
Rotacija nekog objekta obavit će se na način da se primjenom gornje jednadžbe rotiraju sve njegove točke.
Transformacijom rotacije
definirana je rotacija točke V oko
ishodišta za kut Θ. Koodinate točke V' koja nastaje rotacijom točke V oko
ishodišta za kut Θ mogu se izračunati na sljedeći način:
x’ = x cos Θ + y
sin Θ
y’ = -x
sin Θ
+ y cos Θ
Sažetiji način zapisa ovog proračuna u homogenom prostoru može se izvesti ako definiramo matricu rotacije R na sljedeći način:
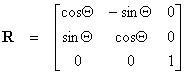
U homogenom prostoru možemo odabrati vrijednost dodatne koordinate npr. iznosa 1 pa matrična jednadžba za proračun koordinata transformirane točke ima sljedeći oblik:
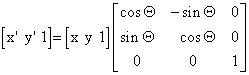
Ovakva jednadžba može se napisati u sažetom obliku na sljedeći način:
V’ = V R
Translacija nekog objekta obavit će se na način da se primjenom gornje jednadžbe translatiraju sve njegove točke.
Transformacija promjene faktora
proporcionalnosti za faktor Sx u smjeru koordinatne osi x
i za za faktor Sx u smjeru koordinatne osi y definirana
je sljedećim jednadžbama:
x’ = x Sx
y’ = y Sy
Sažetiji način zapisa ovog proračuna u homogenom prostoru može se izvesti ako definiramo matricu promjene faktora proporcionalnosti S na sljedeći način:
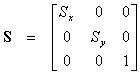
U homogenom prostoru možemo odabrati vrijednost dodatne koordinate npr. iznosa 1 pa matrična jednadžba za proračun koordinata transformirane točke ima sljedeći oblik:
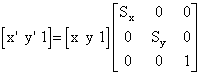
Ovakva jednadžba može se napisati u sažetom obliku na sljedeći način:
V’ = V S
Transformacija smika za kut
a
u odnosu na koordinatnu os x i kut
b
u odnosu na koordinatnu os y definirana je sljedećim
jednadžbama:
x’ = x + y tg b
y’ = y +
x tg a
Sažetiji način zapisa ovog proračuna u homogenom prostoru može se izvesti ako definiramo matricu smika D na sljedeći način:
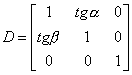
U homogenom prostoru možemo odabrati vrijednost dodatne koordinate npr. iznosa 1 pa matrična jednadžba za proračun koordinata transformirane točke ima sljedeći oblik:
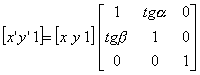
Ovakva jednadžba može se napisati u sažetom obliku na sljedeći način:
V’ = V D
U slučajevima
kad je potrebno izvesti složene transformacije npr. kombinaciju translacije i
rotacije moguće je pristupiti na način da se obavljaju redom pojedine
elementarne transformacije. Međutim, ovaj način zahtijeva velik broj matričnih
množenja. Taj broj se može smanjiti ako se definira matrica složene
transformacije M množenjem matrica pojedinih elementarnih transformacija
M1, M2, ... Mn. Nakon toga se obavlja
množenje vektora pojedinih točaka s matricom složene transformacije.
V’ = V (M1
M2 ... Mn)
V’ = V
M
U 3D
prostoru moguće je definirati rotaciju u odnosu na ishodište oko svake pojedine
koordinatne osi. Točka s koordinatama (x,y,z) iz 3D prostora u homogenom
prostoru predstavljena je vektorom [x1 x2 x3 x4].
Rotacija točke oko osi x za kut
Θ
(kut njihanja ili kut nutacije) definirana je u homogenom prostoru sljedećom
transformacijskom matricom:
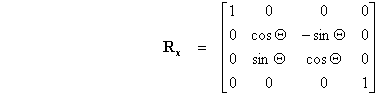
U homogenom prostoru možemo odabrati vrijednost dodatne koordinate npr. iznosa 1 pa matrična jednadžba za proračun koordinata transformirane točke ima sljedeći oblik:
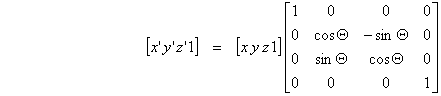
Ovakva jednadžba može se napisati u sažetom obliku na sljedeći način:
V’ = V Rx
Rotacija točke oko osi y za kut j (kut vlastite vrtnje) definirana je u homogenom prostoru sljedećom transformacijskom matricom:
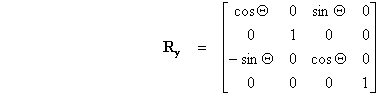
U homogenom prostoru možemo odabrati vrijednost dodatne koordinate npr. iznosa 1 pa matrična jednadžba za proračun koordinata transformirane točke ima sljedeći oblik:
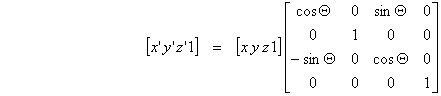
Ovakva jednadžba može se napisati u sažetom obliku na sljedeći način:
V’ = V Ry
Rotacija točke oko osi z za kut f (kut precesije) definirana je u homogenom prostoru sljedećom transformacijskom matricom:
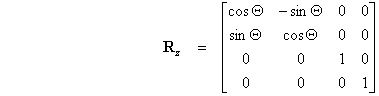
U homogenom prostoru možemo odabrati vrijednost dodatne koordinate npr. iznosa 1 pa matrična jednadžba za proračun koordinata transformirane točke ima sljedeći oblik:
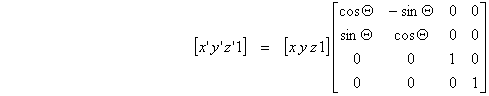
Ovakva jednadžba može se napisati u sažetom obliku na sljedeći način:
V’ = V Rz
Povratak na: Početak stranice | Sadržaj
![]()
![]()
![]() ||| Natrag: Uvod:
Matematički pristup računarskoj grafici
| Gore: Matematički
temelji računarske grafike
|
Naprijed: Projekcije
|
||| Natrag: Uvod:
Matematički pristup računarskoj grafici
| Gore: Matematički
temelji računarske grafike
|
Naprijed: Projekcije
|
Inženjerska grafika, Copyright © D.Begusic